Automated Method to Analyze Geometry and Topology of Mitral Valve Fibrous Ring
The design of prosthetic rings for the annuloplasty of mitral valve fibrous ring (MVFR) was developed from the intuitive to that based on the theoretical analysis of the geometry and topology using the modern technologies of image processing and analysis. The paper presents an automated method of three-dimensional echocardiography data processing and analysis followed by findings fitting.The technique includes several steps. At first, we detected the boundaries of the data obtained by transesophageal three-dimensional echocardiography followed by Procrustes analysis and the mean shape search based on the available data bulk. The method enables to analyze better MVFR geometry, develop MVFR models on the basis of the obtained data, and subsequently, use them to design a prosthetic ring in order to reduce the number of possible complications. Three approximation methods (piecewise cubic, general polynomial, Gauss–Fourier method) were applied for the optimization of the technique results. Each of the methods has its own unique set of advantages and disadvantages, and depending on the task, one can use a certain technique when analyzing or reconstructing MVFR geometry. Thus, it is a powerful tool for MVFR study and prosthetic ring modeling.
Mitral valve (MV) repair using mitral valve fibrous ring (MVFR) annuloplasty is a gold standard in MV insufficiency treatment [1]. The technique first suggested by Alan Carpentier in 1968 was subsequently widely used in cardiac surgery practice [2]. It enables to achieve satisfactory clinical short- and long-term results. However, there are some complications, which worsen a long-term prognosis [3]. One of the most common complications is paravalvular fistula [4]. According to the studies carried out [5–7], it results from a prosthetic ring separation from MVFR, which frequently occurs due to the mismatch of their geometry owning to the prosthesis design imperfection.
Ultrasonic imaging development has contributed to the problem solution. Three-dimensional echocardiography [8] was first used in late 1980s for MV function study, and helped to detect saddle-shape MVFR consisting in the projection of the anterior and posterior cusps in relation to the plane of commissures. In 2003 there was shown the effect of a saddle-form on the strain in the cusps, and therefore, on the longevity of mitral valvular apparatus [9]. It has taken attention to the MVFR anatomy study using modern techniques of image processing and designing [10]. The study of geometry and improvement of MVFR analysis and modeling methods combined with the strain modeling in valvular cusps using a finite element method can contribute significantly to the development of a new generation prosthetic MVFR.
The aim of the investigation was to develop a technique for enhanced study of mitral valve fibrous ring anatomy according to three-dimensional echocardiography based on original algorithm to calculate the fibrous ring geometry using Procrustes analysis and approximation of the findings.
Materials and Methods. 10 patients with coronary heart diseases and no signs of MV damage underwent transesophageal three-dimensional echocardiography. The study complies with the declaration of Helsinki (adopted in June, 1964 (Helsinki, Finland) and revised in October, 2000 (Edinburg, Scotland)) and was approved by the Ethics Committee of Scientific Research Institute of Complex Problems of Cardiovascular Diseases. All patients gave their written informed consent.
We analyzed the data of both: an ejection period of a systolic phase, and also a filling period of a diastolic phase, the periods corresponding to maximal close and open MV states. The data were obtained using QLAB software (Philips, Netherlands) with further export in MATLAB R2015a (MathWorks, USA) for further mathematical processing.
MVFR geometry for each patient was designed using an algorithm for boundary separation from initial data bulk (Figure 1). The boundary was separated in such a way that the number of points was similar among all the rings in a group. We first calculated the number of points needed for the fullest boundary separation from initial three-dimensional data, and then we chose the fewest number (n) among them. Based on three-dimensional data of the rest patients we detected the boundary in such a way that the number of points was equal to n by decreasing the detection detalization. The MVFR average geometry for each group was calculated by computing an arithmetic mean of coordinates of the corresponding points in all patients. The center of the ring mass was determined as a point equidistant from all the points in a ring. The sets of initial data points were converted so that their mass centers matched. After that the rings were turned in such a way that a sum of squared distances to Oxy-surface was the lowest for each ring taken separately. Then we chose a reference standard, and all the rings were turned relative to it so that the sum of squared distances between the points corresponding to each other was the lowest. Then we searched through all the rings as a reference standard, and finally we chose a ring to be a final standard, in which the sum of squared distances between the corresponding points calculated in all other patients appeared to be the lowest. The average geometry was then curve approximated using three methods: 1) piecewise cubic splines; 2) general polynomial; 3) Gauss–Fourier method.
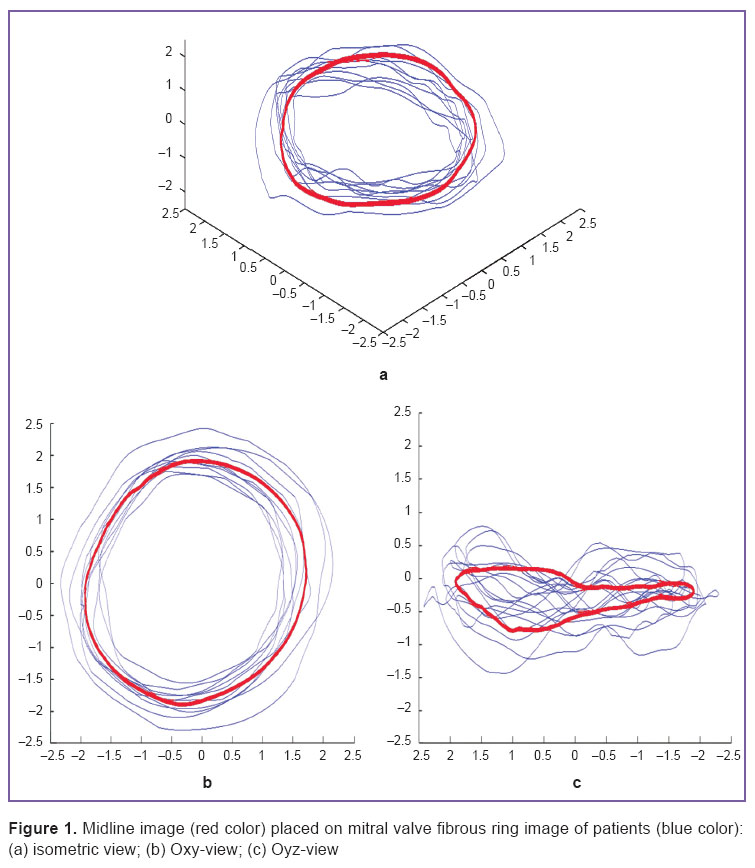 Figure 1. Midline image (red color) placed on mitral valve fibrous ring image of patients (blue color): (а) isometric view; (b) Oxy-view; (c) Oyz-view Figure 1. Midline image (red color) placed on mitral valve fibrous ring image of patients (blue color): (а) isometric view; (b) Oxy-view; (c) Oyz-view
|
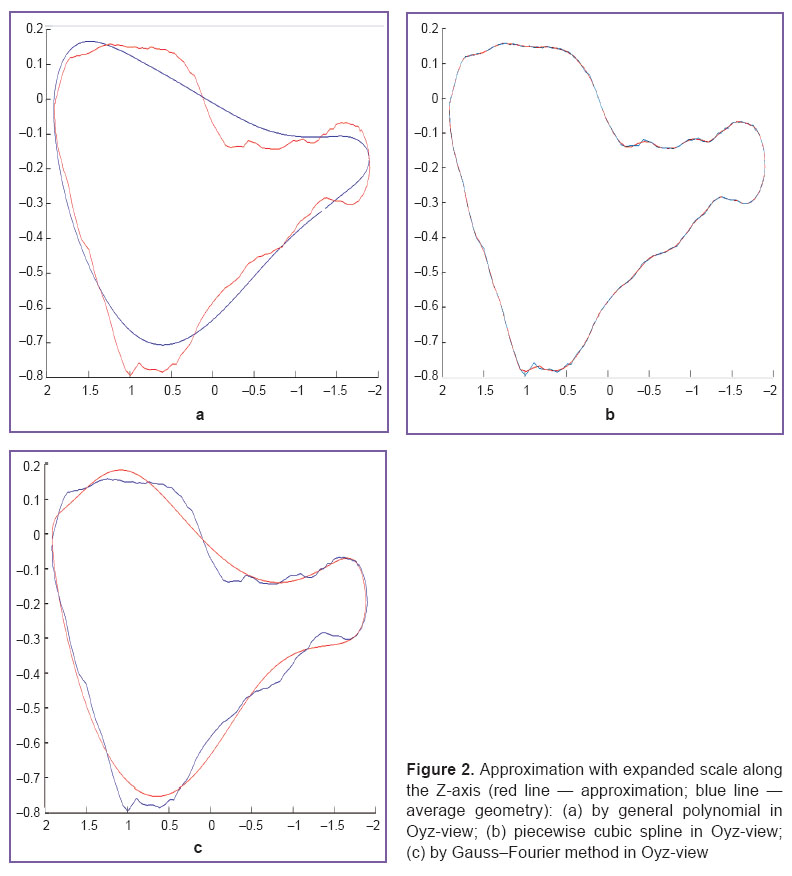
To plot an approximation curve (Figure 2) we calculated a ring perimeter, height, a point with maximal Z-coordinate, commissural width (CW), the annular height to commissural width ratio (AHCWR), two- and three-dimensional MV area. Ring annular height (AH) was determined as the difference between maximal and minimal Z-coordinates, commissural width was calculated as the distance between the commissures. To evaluate MV planarity degree, we calculated the annular height to commissural width ratio, AHCWR=100%·AH/CW. Two-dimensional MV area was calculated as the projected area on Oxy surface, the tree-dimensional MV area being calculated using initial data triangulation before a ring was separated. The described parameters were calculated in each of 10 rings for an ejection period of a systolic phase and a filling period of a diastolic phase. To describe the findings we calculated a median, 95% confidence interval (95% CI) for median, 25 and 75 percentiles, the lowest and the highest sample values.
All mentioned parameters for initial MVFR curves were compared with similar parameters for an approximation curve. Moreover, the parameters for initial and approximation curves were compared in both periods: in an ejection period of a systolic phase, and a filling of a diastolic phase. In both cases we used Mann–Whitney test in the comparison. The differences were considered significant if p<0.05.
Results and Discussion. The developed algorithm for boundary separation enables to separate the most informative set of points rather than a fixed set of equidistant points as shown in the work [10]. We used a generalized Procrustes analysis, which is a modern method for image analysis and processing. Moreover, the novelty of the approach in our study consists in the automated calculation of MVFR average geometry (See Figure 1) with the following approximation of the findings using different techniques (See Figure 2). Using the developed method it becomes possible to carry out a detailed and stiffly accurate comparative analysis of fibrous ring geometry in MV with and without pathology.
The analysis of the findings of three approximation methods used within the framework of the present study showed that due to these methods we can achieve high precision in calculations compared to the technique described in the work [10].
In approximation by Gauss–Fourier method (Figures 3, 4) we plotted a curve with the fewest number of coefficients by means of which we can restore the interpolant itself without resort to the use of specialized software or specific skills, however, the technique exhibited the lowest maximal accuracy and long time of operation in case of large bulk of initial data.
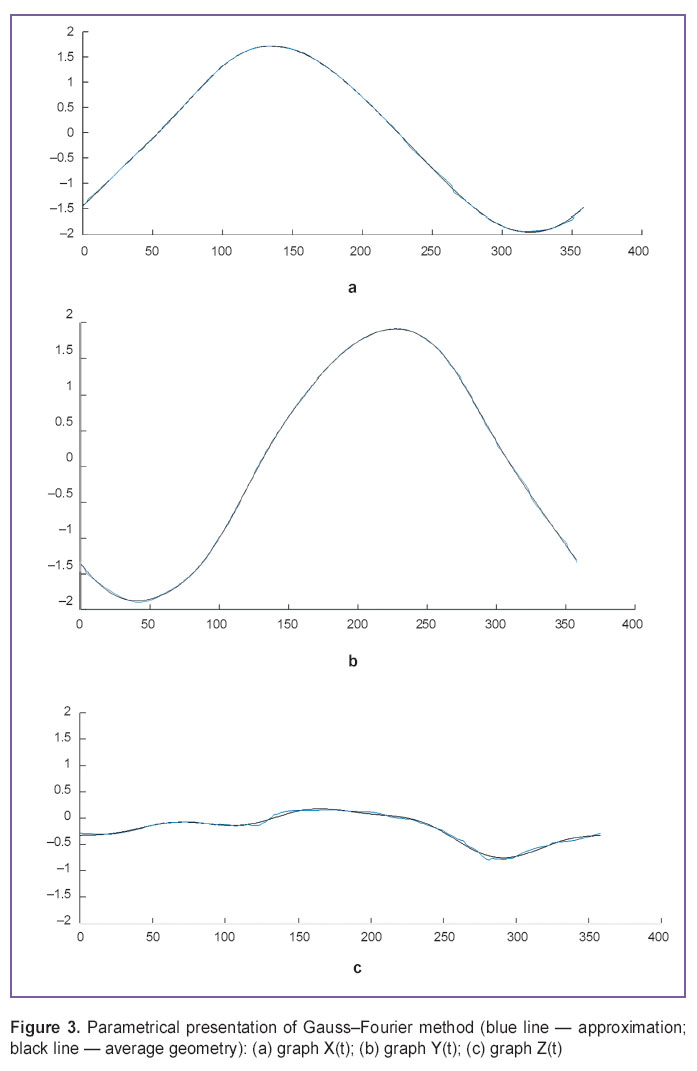 Figure 3. Parametrical presentation of Gauss–Fourier method (blue line — approximation; black line — average geometry): (а) graph X(t); (b) graph Y(t); (c) graph Z(t) Figure 3. Parametrical presentation of Gauss–Fourier method (blue line — approximation; black line — average geometry): (а) graph X(t); (b) graph Y(t); (c) graph Z(t)
|
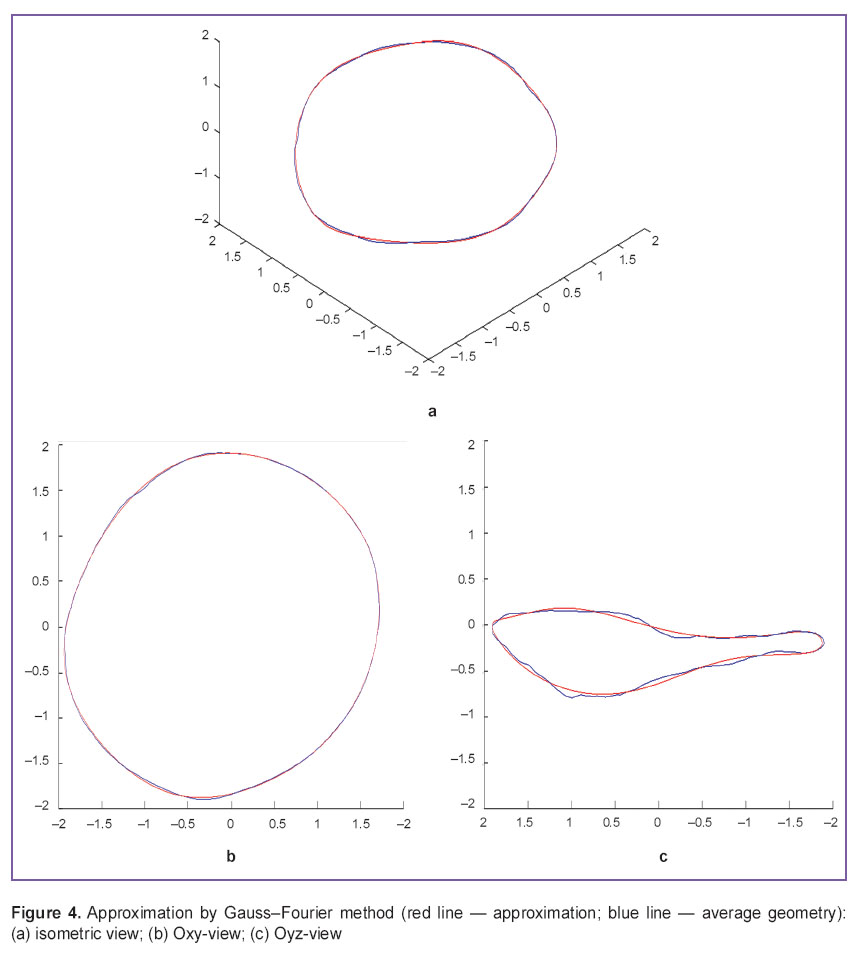 Figure 4. Approximation by Gauss–Fourier method (red line — approximation; blue line — average geometry): (а) isometric view; (b) Oxy-view; (c) Oyz-view Figure 4. Approximation by Gauss–Fourier method (red line — approximation; blue line — average geometry): (а) isometric view; (b) Oxy-view; (c) Oyz-view
|
Piecewise cubic approximation, the most common current method (Figure 5), enables to achieve the highest accuracy, though a relatively large number of approximation coefficients appear resulting in complications when reproducing the bulk data processing in other programs and computer-aided design systems (CAD systems).
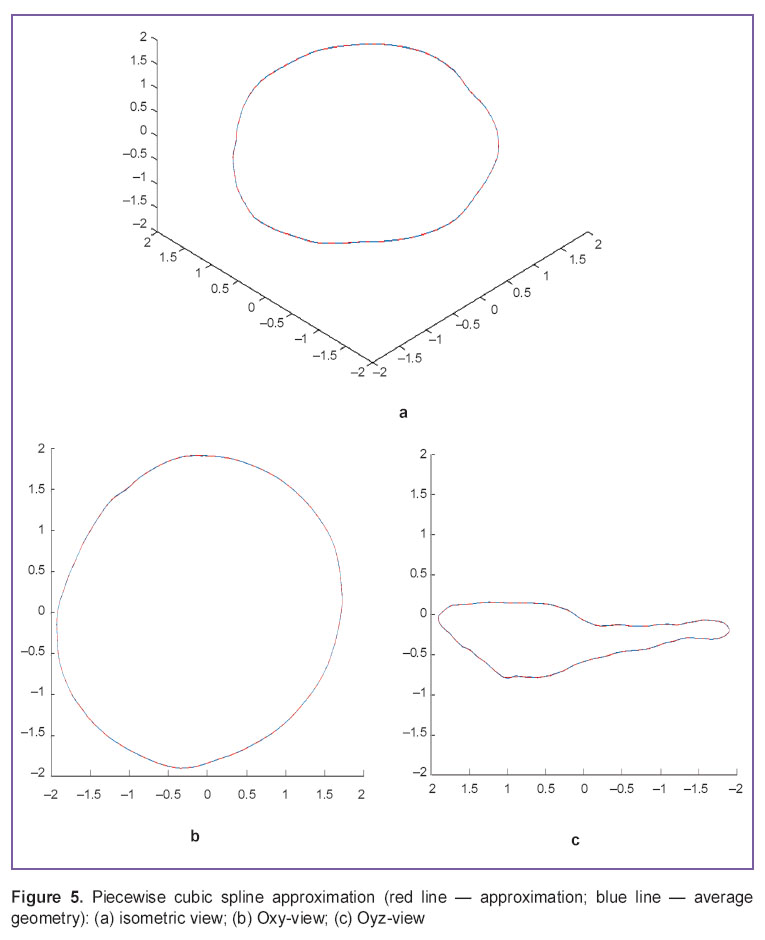 Figure 5. Piecewise cubic spline approximation (red line — approximation; blue line — average geometry): (а) isometric view; (b) Oxy-view; (c) Oyz-view Figure 5. Piecewise cubic spline approximation (red line — approximation; blue line — average geometry): (а) isometric view; (b) Oxy-view; (c) Oyz-view
|
In addition, we used the approximation by general polynomial (Figure 6). The methods is less cumber some, has well known properties, and its usage in further calculations is the simplest. However, it has high variation, poor extrapolation and bad quality in approximation boundary areas.
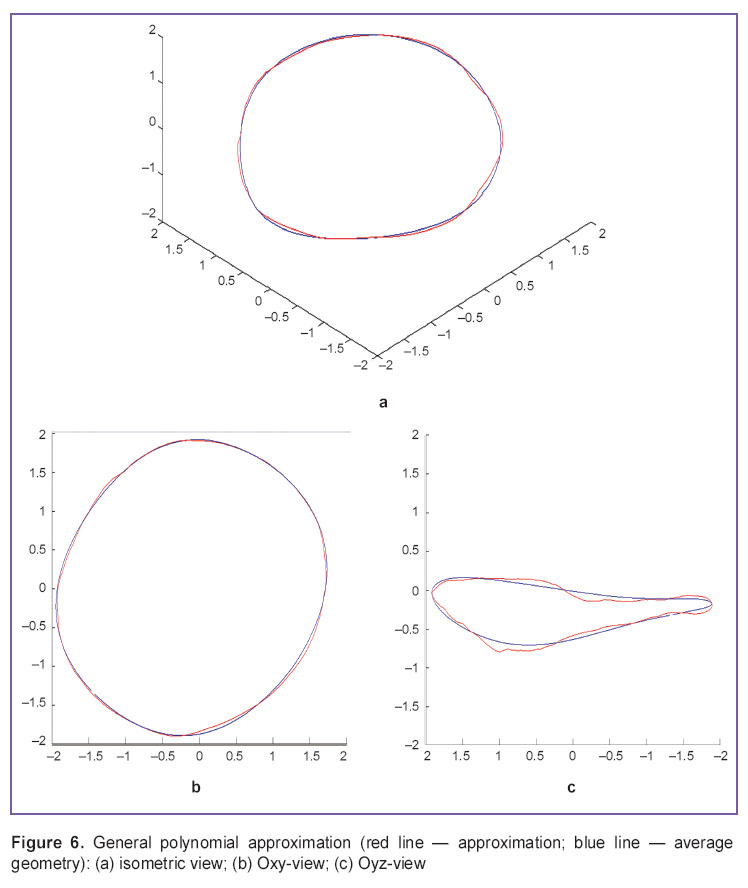 Figure 6. General polynomial approximation (red line — approximation; blue line — average geometry): (а) isometric view; (b) Oxy-view; (c) Oyz-view Figure 6. General polynomial approximation (red line — approximation; blue line — average geometry): (а) isometric view; (b) Oxy-view; (c) Oyz-view
|
The findings suggest that depending on the tasks and requirements to the results when analyzing and reconstructing MVFR geometry any given approximation technique can be used. In order to achieve the required accuracy we can vary the approximation parameters.
The comparison of the curves plotted (Tables 1–3) enabled to reveal significant differences in perimeter, annular height, annular height to commissural width ratio (AHCWR) and no significant differences in such parameters as mitral commissural diameter, two- and three-dimensional MV area. For reasons given we can conclude that during the change from systole to diastole there are significant alterations only in perimeter, annular height, and AHCWR.
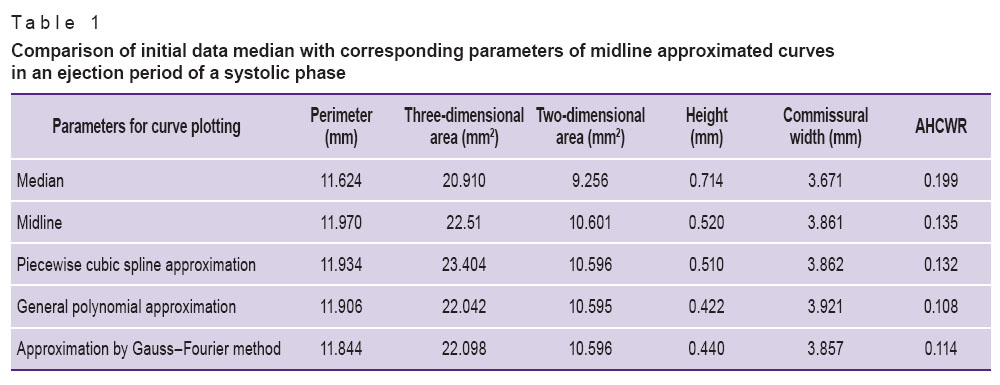 Table 1. Comparison of initial data median with corresponding parameters of midline approximated curves in an ejection period of a systolic phase Table 1. Comparison of initial data median with corresponding parameters of midline approximated curves in an ejection period of a systolic phase
|
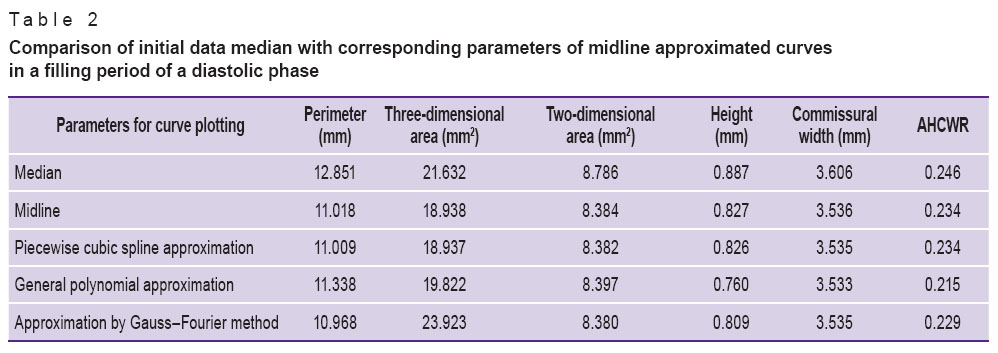 Table 2. Comparison of initial data median with corresponding parameters of midline approximated curves in a filling period of a diastolic phase Table 2. Comparison of initial data median with corresponding parameters of midline approximated curves in a filling period of a diastolic phase
|
 Table 3. Compared results of parameters (p) for initial curves in an ejection period of a systolic phase and in a filling period of diastolic phase using Wilcoxon criterion Table 3. Compared results of parameters (p) for initial curves in an ejection period of a systolic phase and in a filling period of diastolic phase using Wilcoxon criterion
|
This comparison technique of geometry and typology can be further used to analyze MVFR geometrical differences in various pathologies. The findings enable to develop new generation prosthetic rings taking into consideration all geometric peculiarities of MVFR.
Conclusion. The automated method for processing and analysis of three-dimensional echocardiography data followed by the findings approximation enables to calculate quickly and accurately mitral valve fibrous ring geometry, as well as use for such analysis the differences between the average ring shape and the shape in the presence or absence of mitral valve pathology. The technique application can have significant influence when developing new generation prosthetic rings.
Study Funding and Conflicts of Interest. The study was not funded by any sources, and the authors have no conflicts of interest related to the present study.
References
- Andreas M., Doll N., Livesey S., Castella M., Kocher A., Casselman F., Voth V., Bannister C., Encalada Palacios J.F., Pereda D., Laufer G., Czesla M. Safety and feasibility of a novel adjustable mitral annuloplasty ring: a multicentre European experience. Eur J Cardiothorac Surg 2016; 49(1): 249–254, http://dx.doi.org/10.1093/ejcts/ezv015.
- Carpentier A. Reconstructive valvuloplasty. A new technique of mitral valvuloplasty. Presse Med 1969; 77(7): 251–253.
- Lee L.S., Kwon M.H., Cevasco M., Schmitto J.D., Mokashi S.A., McGurk S., Cohn L.H., Bolman R.M. 3rd, Chen F.Y. Postoperative recurrence of mitral regurgitation after annuloplasty for functional mitral regurgitation. Ann Thorac Surg 2012; 94(4): 1211–1216, http://dx.doi.org/10.1016/j.athoracsur.2012.05.005.
- García E., Sandoval J., Unzue L., Hernandez-Antolin R., Almería C., Macaya C. Paravalvular leaks: mechanisms, diagnosis and management. EuroIntervention 2012; 8(Suppl Q): Q41–Q52, http://dx.doi.org/10.4244/EIJV8SQA9.
- Tsuneto A., Eishi K., Miura T., Tanigawa K., Matsukuma S., Minami T., Koide Y., Ikeda S., Kawano H., Maemura K. Comparison of saddle-shape flexibility and elliptical-shape stability between Cosgrove-Edwards and Memo-3D annuloplasty rings using three-dimensional analysis software. Gen Thorac Cardiovasc Surg 2016 Apr 6, http://dx.doi.org/10.1007/s11748-016-0645-0. [Epub ahead of print].
- Carpentier A. Mitral valve annuloplasty. Ann Thorac Surg 1990; 49(3): 508–509, http://dx.doi.org/10.1016/0003-4975(90)90277-d.
- Owais K., Montealegre-Gallegos M., Jeganathan J., Matyal R., Khabbaz K.R., Mahmood F. Dynamic changes in the ischemic mitral annulus: implications for ring sizing. Ann Card Anaesth 2016; 19(1): 15–19, http://dx.doi.org/10.4103/0971-9784.173014.
- Bayramoğlu A., Taşolar H., Otlu Y.Ö., Hidayet Ş., Kurt F., Doğan A., Pekdemir H. Assessment of left atrial volume and mechanical functions using real-time three-dimensional echocardiography in patients with mitral annular calcification. Anatol J Cardiol 2016; 16(1): 42–47, http://dx.doi.org/10.5152/akd.2015.5897.
- Salgo I.S., Gorman J.H. 3rd, Gorman R.C., Jackson B.M., Bowen F.W., Plappert T., St John Sutton M.G., Edmunds L.H. Jr. Effect of annular shape on leaflet curvature in reducing mitral leaflet stress. Circulation 2003; 106(6): 711–717, http://dx.doi.org/10.1161/01.cir.0000025426.39426.83.
- Pouch A.M., Vergnat M., McGarvey J.R., Ferrari G., Jackson B.M., Sehgal C.M., Yushkevich P.A., Gorman R.C., Gorman J.H. 3rd. Statistical assessment of normal mitral annular geometry using automated 3D echocardiographic analysis. Ann Thorac Surg 2014; 97(1): 71–77, http://dx.doi.org/10.1016/j.athoracsur.2013.07.096.