Diagnosis of a Disease Using the Values of Statistical Functionals Calculated from Infrared Spectroscopic Parameters of Blood

In mathematics, the values of analyzed body parameters can be considered as random variables (RV). Obviously, any developing disease is associated with the summation of the RV, observed in normal health, with the RV related to the disease. It seems reasonable to argue that the disease-induced changes in biological processes, at least at an early stage of the disease, will be statistically independent (or almost independent) on the biological processes found in a healthy person. Consequently, this property must also hold for the factors reflecting the results of medical tests.

Earlier we presented a method of mathematical processing of data obtained from infrared (IR) spectra of patients with vibration disease [1]. As a continuation of that study, a mathematical analysis of the IR spectra of patients with brain tumors has been conducted. In this report, an improved version of the technique [1] is used (the modified mathematical approach is described earlier [2]).

The aim of the study was to identify the characteristics of statistical functionals calculated from the set of infrared spectroscopic parameters of the blood obtained from a blood sample of a patient.

Materials and Methods. A single-blind prospective cohort study was conducted in 43 patients with malignant brain formations hospitalized in the Nizhny Novgorod Interregional Neurosurgical Center and at the Privolzhsky Federal Medical Research Center between 2009 and 2013. The patients’ blood serum samples were analyzed using IR spectroscopy [3].

The study was conducted in accordance with the Helsinki Declaration adopted in June 1964 (Helsinki, Finland) and revised in October 2000 (Edinburgh, Scotland) and approved by the Ethics Committee of the Privolzhsky Federal Medical Research Center. An informed consent was obtained from each patient.

Based on the results published earlier [1, 2], we assume that the biological values analyzed for the purpose of diagnosis can be considered as a sum of random terms (or factors) in the form of:

where x₁(j) and x₂(j) are statistically independent real discrete random processes (random sequences) of the discrete variable j=1, 2, ..., N equal to the number of the measured parameter.

We propose that the random sequence x₁(j) reflects the condition of normal health, whereas the discrete “weak” process x₂(j) (which is usually smaller than x₁(j) except for sporadic peak values) reflect the fluctuations associated with the developing disease. Only the values of x(j) that are equal to x₁(j) in the absence of a disease can be directly measured. Any realization of the process x=x(j) is expressed as a series of values x(1), x(2), …, x(N) obtained from a single analysis of the patient.

We emphasize that the assumed statistical independence of random values x₁ and x₂ is the only hypothesis applied to this study. This hypothesis has been substantiated by the calculations shown below; those are based on the mathematical processing of large arrays of the experimental data accumulated so far. The algorithm used in this case is not by itself connected to this hypothesis; rather we need this hypothesis to explain the obtained results.

For each series x(1), x(2), …, x(N) we split the range of values [x_min, x_max] (where the limits represent the minimum and maximum values of RV x for a given series) into intervals with the same length Δ:

The Δ value, one and the same for all realizations, will be specified further when performing a numerical calculation. The value of N₀ is an RV, i.e., a value own for each separate analysis.

We now compare RV x with another RV w, equal to the number m of the interval with limits

in which the measured value of x falls. The respective probability density ρ(w) can be expressed in the following form:

Here any coefficient P_m is the probability that the value of x falls into the interval (3) with number m, and δ(w–m) is the Dirac delta function. The values of P_m obey the condition of normalization:

By analogy, the probability densities ρ_{1, 2}(w) for RV х_{1, 2} relating to the random processes x_{1, 2}(j) can be determined in the similar way.

Of note, the functions ρ(w), ρ₁(w) and ρ₂(w), correspond to the set of values of the random processes x(j), x₁(j), and x₂(j), respectively, within a limited number of values of index j=1, 2 , ..., N. Therefore, the indicated probability densities themselves are random functions of the variable w, and may differ for each and every series of values x(j), i.e. for each analysis.

Taking into account that the x₁(j) and x₂(j) are independent, the value of ρ(w) corresponding to the selected segment of the realization x(t) can be presented as

The proposed technique will work if the width of the distribution ρ₂(w), while staying a value much smaller than the horizontal scale of the probability density ρ₁(w) changes, nevertheless significantly (with a high probability) exceeds the size of small-scale fluctuations of the given function. (The validity of this assumption is confirmed by the below numerical calculations.) Notably, the integration (5) can be viewed as averaging the factor ρ₁(w–w’) over the probability density ρ₂(w’). Obviously, under the given conditions, this averaging will result in a decrease in the amplitude of these small-scale fluctuations.

In Figure 1 (a), the black curve illustrates the probability density distribution ρ(w)=ρ₁(w) given that x₂(j) is identically equal to 0. The blue line represents the “averaging” probability density ρ₂(w) corresponding to a diseased state. For the sake of simplicity, both functions are shown as continuous lines, while in this report we operate with their discrete analogs. Figure 1 (b) schematically shows the probability density ρ(w) in the presence of process x₂(j). Obviously, for a sufficiently large value of N, much smoother values of ρ(w) corresponding to a specific blood test, can signify the process x₂(j), in contrast with the typical ρ(w) distribution when x₂(j) is identically equal to 0.

---

Figure 1. Roughness of the schematic graphs showing the probability density for the measured biological random variable (RV) in the absence or presence of a disease: (a) is a schematic plot of the probability density of the measured RV in health (the wide black curve ρ(w)=ρ1(w), corresponding to the condition x=x1(j) and x2(j)=0 for all j) and a plot of the probability density corresponding to fluctuations in the measured biological parameters associated solely with the presence of a disease (the blue curve ρ2(w) corresponding to x2(j)≠0); (b) is a schematic view of the probability density ρ(w) of the measured biological RV in the presence of a disease, when in the general case x2(j)≠0 and x=x1(j)+x2(j); (c) is a schematic view of the probability density for the RV X=sin(x) in the absence of a disease, when x=x1(j) and identically x2(j)=0; (d) is a schematic view of the probability density for the RV X=sin(x) in the presence of a disease, when x2(j)≠0 and x=x1(j)+x2(j)

---

The difference of that type, from the mathematical point of view, must lead to changes in the properties of the Fourier transform corresponding to the ρ(w) function, in other terms, the characteristic function below:

This function is relevant to any blood test and, obviously, reflects a random process of the dimensionless Fourier variable p. It is well known that the Fourier transform depends very strongly on the smoothness of the prototype represented by the random function ρ(w). Therefore, the Fourier transform can (with a high probability) become sensitive to the presence or absence of small-scale fluctuations in the P_m coefficients (for more details, see [1]).

We note that upon turning from a random process (1) to a nonlinear process

the differences in the properties of the functions L(p) in the presence or in the absence of the term x₂(j) in equation (1) can only rise. Indeed, taking into account the properties of the probability density of functions of RV [4], it is easy to show that the probability density ρ_X(w) corresponding to RV of X in equation (7) turns out to be proportional to the factor , i.e. contains integrable characteristics at the limit points of the range of the argument w∈ [–1.1]. Consequently, for values of w close to unity, the amplitude of small-scale fluctuations increases sharply. Accordingly, the difference in the properties of the Fourier transform L(p) increases in the absence or, conversely, in the presence of a disease.

In Figure 1 (c), at w≥0, the probability density ρ_X(w) for the condition that x₂(j) is identically equal to 0 is schematically shown; in Figure 1 (d) — the same function in the presence of the process x₂(j). The curves for ρ_X(w) in Figure 1 (c) and (d) are mathematically equivalent to the graphs of the function ρ(w) in Figure 1 (a) (black curve) and Figure 1 (b). When compared, the curve in Figure 1 (c) has a much higher degree of roughness than that in Figure 1 (a); as a consequence, there is a much greater difference between Figure 1 (c) and (d), than between Figure 1 (a) and (b). Therefore, with a sufficiently high probability, the difference between the L(p) Fourier transforms corresponding to Figure 1 (c) and (d) will be larger than that between the functionals related to Figure 1 (a) and (b).

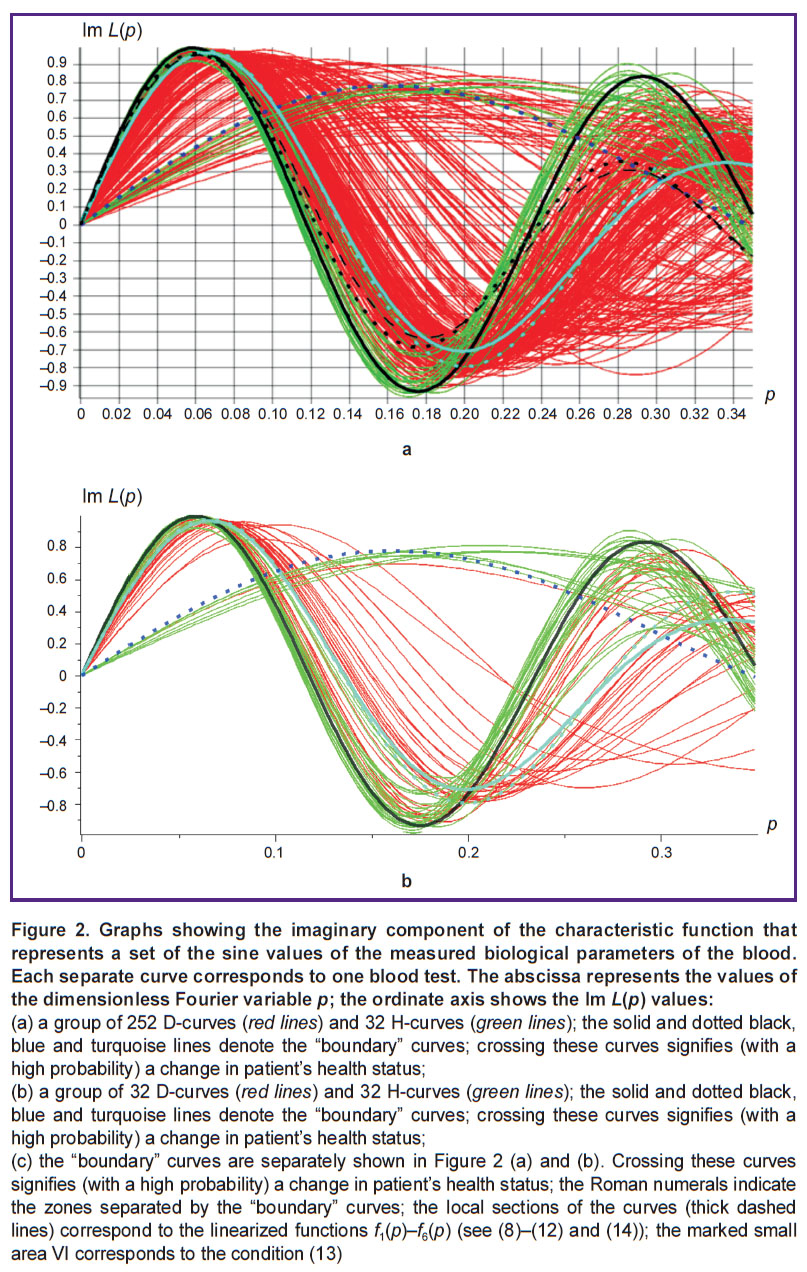
Results and Discussion. The presented graphs reflect the characteristic functions derived from the data of the IR study on blood serum [3] conducted in accordance with report [5] (Figures 2–4). Each curve corresponds to one analysis of one person and is based on 13 values of the amplitude ratios of the absorption peaks (cm^–1/cm^–1): 1 — 1,165/1,160; 2 — 1,165/1,070; 3 — 1,165/1,150; 4 — 1,165/1,140; 5 — 1,040/1,070; 6 — 1,165/1,130; 7 — 1,070/1,025; 8 — 1,165/1,050; 9 — 1,165/1,025; 10 — 1,100/1,050; 11 — 1,170/1,150; 12 — 1,170/1,160; 13 — 1,125/1,165. We realize that such a small number of values is not sufficient to construct the “real” histogram that would reflect the data distribution practically insensitive to changes in the RV realization form. Yet, the proposed methodology requires only that each new data set x(j) would have a respective random functional (for example, similar to the characteristic function), whose properties would change with the appearance of the small term x₂ in the right-hand side of equation (1). As further calculations show, within this approach the sample size used here is, in most cases, sufficient.

---

Figure 2. Graphs showing the imaginary component of the characteristic function that represents a set of the sine values of the measured biological parameters of the blood. Each separate curve corresponds to one blood test. The abscissa represents the values of the dimensionless Fourier variable p; the ordinate axis shows the Im L(p) values: (a) a group of 252 D-curves (red lines) and 32 H-curves (green lines); the solid and dotted black, blue and turquoise lines denote the “boundary” curves; crossing these curves signifies (with a high probability) a change in patient’s health status; (b) a group of 32 D-curves (red lines) and 32 H-curves (green lines); the solid and dotted black, blue and turquoise lines denote the “boundary” curves; crossing these curves signifies (with a high probability) a change in patient’s health status; (c) the “boundary” curves are separately shown in Figure 2 (a) and (b). Crossing these curves signifies (with a high probability) a change in patient’s health status; the Roman numerals indicate the zones separated by the “boundary” curves; the local sections of the curves (thick dashed lines) correspond to the linearized functions f1(p)–f6(p) (see (8)–(12) and (14)); the marked small area VI corresponds to the condition (13)

---

Figure 3. Graphs of the functional q(p) of the imaginary part of the characteristic function, representing the sine values of the measured blood parameters; see (15). The group of green lines includes 26 curves; the graphs corresponding to the 6 green lines passing through the upper part of Figure 2 (a) are excluded from this illustration: (a) the complete set of 252 D-graphs (red lines) and 26 H-graphs (green lines) reflecting the functional q(p) of the imaginary part of the characteristic function that represents the sine values of the measured blood parameters; each separate curve corresponds to one blood test; the abscissa — the values of the dimensionless Fourier variable p; the ordinate — the values of q(p); (b) a group of D-graphs (red lines) and 26 H-graphs (green lines) reflecting the functional q(p) of the imaginary part of the characteristic function that represents the sine values of the measured blood parameters; only the red D-curves that pass through the inaccessible for analysis in Figure 2 (a) zones VII, VIII, and IX (see Figure 2 (c)) are shown; the group of green lines in Figure 3 (b) is the same as in Figure 3 (a); the abscissa — the values of the dimensionless Fourier variable p; the ordinate — the values of q(p)

---

Figure 4. Graphs of the module |L(p)| of the characteristic function, representing the plurality of the sine values obtained from the measured blood parameters: (a) 252 D-curves (red lines) and 32 H-curves (green lines) for the graphs of the module |L(p)|; the abscissa — the values of the dimensionless Fourier variable p; the ordinate — the |L(p)| values; the black circles outline the points of condensation of the red lines (D-curves) with the complete absence of green curves (H-curves) in these areas; the blue oval marks the area with 5 points of condensation: non-passing through at least one of these points indicates (with a high probability) the existence of a D-curve; (b) this graph is similar to Figure 4 (a), but it depicts only those red curves that enter the zone of green lines in Figure 2 (a), and therefore are hardly accessible for analysis based on methodology pertaining to this Figure; the area encircled with a black line contains the condensation point of the red curves (1.571, 0.077); the remaining points of condensation of the red lines that occur in Figure 4 (a), are absent here; the group of green lines is the same as in Figure 4 (a)

---

We also note that when calculating a set of intervals of the form (3), its own for each separate blood test, when replacing the random process x(j) by X(j) [see equation (7)], the least value X_min=min{X(j)} is given in place of x_min. This minimum is selected by aggregating the 13 sine values of the peak-to-peak ratios presented above, as well as 14 more sine values from the actual peak amplitudes expressed in cm^–1. Such a choice of X_min, as shown by numerical calculation, leads to the most profound difference between the two group of statistical functionals of the form (6), corresponding to the presence or, on the contrary, the absence of a disease. Further calculations are related only to the statistics of the peak-to-peak sines.

Figure 2 shows the graphs of the imaginary part of the characteristic function Im L(p). We performed calculations for the function sin(x(j)) at Δ=1/15 [see equation (2)]. In Figure 2 (a) and (b), all green curves, dotted blue, as well as solid and dashed turquoise lines correspond to the normal state of health, whereas all red and all black (solid, dotted and dashed) graphics correspond to the oncological brain disease. In Figure 2 (a), the number of curves corresponding to the healthy condition (hereinafter referred to as H-curves or H-graphs) is 32, and the number of curves corresponding to the disease (hereinafter D-curves or D-graphs) is 252. Figure 2 (b) shows 32 curves of both types; this Figure makes it possible to better represent the distribution of the H- and D-curves.

The indicated graphs (dotted blue, solid and dotted turquoise, and also solid black) are boundary curves that mark the limits beyond which it becomes possible to draw conclusions about the patient’s health with a probability close to unity (interpretation of the dotted and dashed black curves is discussed below). In Figure 2 (c), these four boundary curves are given separately. In addition, the dotted lines depict those local fragments of the function graphs, which mathematically approximate these boundary lines at the respective sections of the abscissa axis.

In the Fourier-variable domain p∈[0.111; 0.137] any descending curve passing above the lines of continuous and dashed turquoise graphs (within this interval these two curves almost merge and intersect) with a probability of at least P₁=32/33≈0.97, indicates the presence of the disease. This statement results from the fact that none of these 32 H-graphs has the property of passing (in the indicated range of the Fourier variables) above these two lines while descending, and all curves having this property are D-graphs. The respective area is marked with the Roman numeral I on the Cartesian plane (see Figure 2 (c)).

With respect to the interval under consideration, p∈[0.111; 0.137], we get the approximating function:

In Figure 2 (c), the graph of this function, in the indicated range of values of the Fourier variable, is shown with a dashed yellow line. Obviously, within the given interval it is almost identical to the solid and dashed turquoise boundary curves. Thus, if (within the considered segment of the abscissa) the graph of the imaginary part of the characteristic function lies above f₁(p) and still descends, it can be concluded (with a probability not lower than P₁) that this is a D-curve.

Recalling the above reasoning and calculations, let us consider the angular sector filled with red D-curves and with the center placed at the origin (see Figure 2 (a); in Figure 2 (c), this section is marked with the Roman numeral II). For the lower boundary of this angular sector (shown with the dashed blue curve) the approximating function for p∈[0; 0.031] can be expressed as:

(see the red dotted line in Figure 2 (c), starting from the origin).

By analogy we define the function

which approximates the solid and dashed turquoise lines on the same segment p∈[0; 0.031] of the abscissa (here, both curves merge into one). Thus, we obtain an approximation for the upper boundary of the angular sector, within which (with probability P₁) only the disease associated red curves are present. The graph of the function f₃(p) for the specified segment of the horizontal axis is shown in Figure 2 (c) (the orange dashed line starting from the origin).

We then come to the following conclusion: if the graph f(p) pertaining to the imaginary part of the characteristic function (derived according to the proposed method) in the interval p∈[0; 0.031], at least for some values of ρ, satisfies the inequality f₂(p)<f(p)<f₃(p), it indicates the presence of a D-curve with probability not less than P₁.

Of note, two sectors I and II shown in Figure 2 (c) almost always correspond to the same D-curves. It is also true for area III with p∈[0.220; 0.345]. This area is located below the dashed turquoise and blue lines, as well as below the solid curves and somewhat to the right of the rightmost set of green curves present in the lower central part of Figure 2 (a). Given the marked coincidence of the D-curves, exploring this area is not expected to provide new information on the probability of the disease. Nevertheless, it seems useful to approximate the respective boundary lines.

Specifically, taking the segment p∈[0.232; 0.262] for the dashed turquoise curve we obtain the below approximating function:

(see the violet dotted line in Figure 2 (c)). Any graph of the imaginary part of L(p) passing below the function f₄(p) at this segment of the abscissa, in the area marked IV in Figure 2 (c) (with probability P₁) can be interpreted as a D-curve.

On the segment p∈[0.307; 0.350] for the dashed turquoise curve, we obtain the below approximating function:

(see the green dotted line in Figure 2 (c)). Any graph of the imaginary part of L(p), which intersects the graph f₅(p) at this section while ascending (see zone V in Figure 2 (c)) is interpreted (with probability P₁) as a D-curve.

We point out that the D-curves (black dashed and dotted, Figure 2 (a)) passing through sectors VII, VIII, and IX also intersect while descending the indicated section of the graph of the function (12); these two curves illustrate the behavior of the D-curves in the indicated three sectors. (Sector IX includes the area between the black line and the closest segments of the two turquoise lines on both sides of the dashed blue curve.) In these three sectors, unlike zones I–VI, all the red curves are mixed with the green ones, which makes it impossible to conclude a priori on the state of patient’s health.

We also note that the small area in the extreme left part of sector III, located at p∈[0.205; 0.210] below the turquoise dashed curve and to the right of the last green curve, which passes through this area in Figure 2 (a) (the zone is marked in Figure 2 (c) with the Roman numeral VI), intersects, among others, several red D-graphs. These graphs intersect the segment located between the points:

(see Figure 2 (a)). In other areas of this Figure, these curves pass through sectors VII, VIII, and IX, which are inaccessible for analysis within the present methodology. The probability that the graph of Im L(p) when crossing sector VI corresponds to a D-curve is also P₁.

Finally, for the section of the black curve corresponding to interval p∈[0.105; 0.129] (see Figure 2 (a)), we find that any graph of the imaginary part of the characteristic function, passing (within the given segment of the abscissa) below the black line in the area X, corresponds to an H-curve with a probability not less than P₂=251/252≈0.99. Consequently, such a graph corresponds (with the indicated probability) either to normal health or at least to the absence of the brain disease in question. This conclusion results from the fact that none of all 252 D-curves passes below the black curve in the indicated range of values of the Fourier variable p. In Figure 2 (c) the turquoise dashed line in the indicated section of the curve corresponds to the approximating function below:

As already noted, in Figure 2 (a) and (b) about a quarter of the red D-curves are located in the area populated by the green H-graphs, specifically the red curves passing through sectors VII, VIII, and IX (see Figure 2 (c)). Obviously, these curves in Figure 2 (a) by themselves cannot indicate the presence or absence of a disease. The rest of the curves (depending on their location in Figure 2 (a)) indicate either the presence (with the probability P₁≈0.97) or the absence (with the probability P₂≈0.99) of a disease in a given patient.

In order to increase the efficacy of the proposed method for detecting a disease, here we analyze a few more applications of the above statistical functionals. For example, in Figure 2 (a), for the values of the Fourier variable p>0.27 the many points of the maxima of the green curves are shifted towards the left as compared with the points of the maxima of the red graphs. (This agrees well with the mathematical properties of the integral convolution 5, whose Fourier transform is equal to the product of the Fourier transforms of the integrands.) In order to understand how this shift of the extremum points can be used for additional diagnosis of blood tests, let’s take a look at Figure 3 (a).

Here, any curve corresponds to function:

which is the same for both green and red graphs and defined in the segment p∈[0.055; 0.070] (the line colors are the same as before). This form of q(p) allows us to clearly identify the zero points of the derivative Im L(p). These points are supposed to correlate with the intersections of the downward narrow peaks; each of these peaks includes a descending segment and an ascending segment, with a horizontal line q=In{10^–6}≈–13.8. Since the graph plotter (which selects the values of the argument p for the function q(p)) cannot precisely pick up the point where the derivative

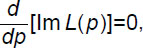
we have to limit our analysis to the level of intersection of these peaks with the horizontal straight line q=–6. As can be seen from this Figure, under the condition p<0.0585 (the area to the left of the vertical blue line), an H-curve occurs with a probability not less than P₂. This implies with the indicated probability, either the normal health or the absence of the brain disease in question. Along with that, in the area where p>0.0664 (to the right of the vertical lilac line) with probability P₃=26/27≈0.96, we can conclude that there is a D-curve there. The value of P₃ is based on the fact that 6 out of the 32 green curves pass through the upper part of Figure 3 (a) and they are also incorporated in the statistical calculations.

In Figure 3 (a), the area most relevant to this analysis, located to the right of the lilac straight line (i.e., where no green graphs exist and which is a highly probable “disease” area), contains no more than half of the plurality of red curves, whereas in Figure 2 (a), in the areas free of green lines, three-fourths of the red curves occur. Therefore, the mathematical approach related to Figure 3 (a), when applied to a specific blood test, can be used as just a supplement to the methodology illustrated in Figure 2 (a). Along with that, it is important to note that part of the red graphs entering the indicated area to the right of the lilac line correspond to the graphs in Figure 2 (a), which are entirely located in areas VII, VIII, and IX that are inaccessible for analysis.

In Figure 3 (b), in contrast to Figure 3 (a), only those red curves are shown that pass through the inaccessible for analysis in Figure 2 (a) zones (VII, VIII, and IX, see Figure 2 (c)). The group of green lines in Figure 3 (b) is the same as in Figure 3 (a). In the area of interest to the right of the vertical lilac line, there are 12 separate red curves (for the sake of illustration, in Figure 3 (a) and (b) the lines are widened, so most of them correspond to two almost merging different curves). Thus, we can conclude that the procedure related to Figure 3 (a) and (b), allows one to diagnose a disease (with a high probability) in about one of five cases inaccessible for the analysis related to Figure 2 (a).

An additional approach may become possible. Let us consider two groups of green and red curves within the interval p∈[0; 3.5] (Figure 4 (a)). Each curve corresponds to the graph of the module |L(p)|. The length of this interval slightly exceeds the half-period of the function L(p) (for p∈[ ; 2] the graph |L(p)| is symmetrical to the graph for the segment p∈[0; ]).

As can be seen from the Figure, there is a point of condensation of the red lines (with a complete absence of green curves) in the center of each of the areas marked with black contours. Their coordinates are: (1.571, 0.077) — the center of the lower black circle; (1.571, 0.414) — the center of the upper black ellipse; (1.046, 0.307) — the center of the left black circle; (2.093, 0.309) — the center of the right black ellipse, and (3.142, 0.692) — the center of the right upper circle. The curves pass through these points with errors equal to the minimum distances from any of them to the corresponding curve, i.e. no more than 0.010.

Consequently, when the graph of |L(p)| that corresponds to the newly obtained blood analysis, passes through any of the five given points, it is a D-curve with a probability at least P₁. Moreover, if such a graph does not pass (with the specified accuracy) through one of the five condensation points with the coordinates (1.571, 0.172), (1.571, 0.230), (1.571, 0.277), (1.571, 0.317), and (1.571, 0.385) located inside the blue oval in Figure 4 (a), this indicates a high probability of a disease.

In contrast to Figure 4 (a), the graph in Figure 4 (b) pertains only to those red curves that fall into the zone of green lines in Figure 2 (a), and are, therefore, inaccessible for analysis by methodology related to this Figure. The black circle denotes the area containing the condensation point of red curves (1.571, 0.077). In this case, the other points of condensation of the red lines (shown in Figure 4 (a)) are absent. Any of the 11 graphs of |L(p)| that passes through this point (or not farther than 0.01 of that point), can be defined (with probability P₁) as a D-curve. Consequently, the approach corresponding to Figure 4 (a) and (b) also allows one to diagnose (with a high probability) the disease in about one fifth of the cases inaccessible for analysis in Figure 2 (a).

Conclusion. Obviously, the above mentioned approaches to the problem of diagnosing a disease using statistical functionals based on blood analyzes and considered random variables, are not the only possible methodology. The authors believe there is a much larger number of these functionals that can significantly change their properties (at least within a small segment of the respective variables) in response to even a small random factor in the blood sample that is associated with a disease and statistically unrelated to the parameters typical for normal health. A common feature of such methods is the transition from the analysis of data directly obtained from medical tests to the analysis of variations in the properties of these statistical functionals.

Study Funding and Conflicts of Interest. The study was not funded by any sources, and the authors have no conflicts of interest related to the present study.