Two-Wavelength Fluorescence Monitoring and Planning of Photodynamic Therapy

Khilov A.V., Loginova D.A., Sergeeva E.A., Shakhova M.A., Meller A.E., Turchin I.V., Kirillin M.Yu.

Key words: photodynamic therapy; planing of photodynamic therapy; fluorescence imaging; chlorine series photosensitizers; Monte-Carlo simulations.

The aim of the study is to develop approaches for fluorescence monitoring and planning of photodynamic therapy employing chlorine series photosensitizers.

Materials and Methods. The study included numerical simulations and experiments with optical agar phantoms of biotissue and human skin in vivo. Fluorescence imaging was used as a method of optical monitoring. Chlorine series photosensitizer Photoditazin (Veta Grand, Russia) was employed. Numerical simulation of light propagation was performed with Monte-Carlo technique for a multilayer skin model.

Results. It was demonstrated that in the case of two-wavelength fluorescence monitoring of photosensitizer penetration into the tissue the ratio of fluorescence signals excited at wavelengths of 405 and 660 nm can be used as a characteristic of photosensitizer penetration depth in biological tissue. The results of numerical simulations are in good agreement with the results of model experiments on agar phantoms and pilot in vivo experiment. Radiant exposure and absorbed light dose maps at the wavelengths of 405 and 660 nm were calculated employing Monte-Carlo technique; the dependencies of the characteristic dose values on the optical properties of the medium were analyzed.

Conclusion. Two-wave fluorescence imaging technique allows for non-invasive estimation of chlorine series photosensitizer penetration depth into the biotissue after topical application, while numerical simulation by Monte-Carlo method allows for more accurate choice of the light exposure dose for photodynamic therapy depending on optical properties of the tissue and the radiation wavelength.

Photodynamic therapy (PDT) is a modern multi-factor method for treatment of tumors and non-tumorous pathologies, based on the selective accumulation of a photosensitizer (PS) in tissues, followed by optical radiation exposure at the absorption wavelength of the PS. Absorption of photons by the PS causes a photodynamic reaction. The main photodynamic effects are chemical impact on cells, tumor vasculature damage and immune reactions [1–3].

PDT has already taken its place in clinical practice and demonstrates high effectiveness in the treatment of a wide range of pathologies. Along with high oncological efficacy PDT also has the potential as a method of antimicrobial therapy in the treatment of inflammatory pathologies of various localizations [4–7].

Talking about the advantages of PDT, such as extremely minor systemic effects, minimal toxicity for healthy tissues, and the possibility of repeating procedure in case of proper indication, its disadvantages should be noted, however. One of the drawbacks of currently used PDT protocols is the fact that only PS dose and light dose are determined when the procedure is planned, without taking into account the individual characteristics of a patient. However, the efficiency of a PDT procedure depends on the distribution of the PS in tissues, the distribution of the absorbed intensity of optical radiation in tissues, and the PS photobleaching under light exposure [8]. The efficiency of a PDT procedure can be increased by taking these factors into account when determining the protocol of the PDT procedure. Therefore, further optimization of PDT technique is recognized as possible and necessary by many researchers [3, 9].

One of the directions of PDT optimization consists in the individualization of the exposure regimes that can be performed due to effective treatment monitoring [3, 10]. Many known approaches use various imaging techniques [11–13]. Optical bioimaging is the most promising among them due to the possibility of real time non-invasive monitoring.

The application of optical bioimaging techniques for monitoring PDT procedure allows controlling PS distribution and photobleaching. Traditionally fluorescence imaging techniques [14] are employed for DT monitoring because PS are fluorescent markers. One of the most popular PSs widely employed in Russia are chlorine series PSs. They feature two maxima corresponding to the wavelengths of 405 and 660 nm in their absorption spectra (Figure 1).

Figure 1. Absorption and emission spectra of chlorine series photosensitizer

Since optical properties of biological tissues at these wavelengths differ significantly (the absorbance at 405 nm is much higher than that at 660 nm [15, 16]), the distribution of exposed intensity (both transmitted and absorbed) is also different, which makes it possible to control the impact depth. Simultaneous use of different PS absorption bands provides additional opportunities for both monitoring and performance of a PDT procedure. In particular, the registration of the fluorescence signal at different excitation wavelengths allows for noninvasive evaluation of PS penetration depth into tissues [17, 18].

In this paper, the aspects of the application of this approach are discussed in a numerical simulation study and in experiments on biotissue phantoms. The difference in absorbed intensity distribution for two wavelengths leads to the difference in the area of impact, which must be taken into account in PDT procedure planning. In this paper, we propose an approach to estimate spatial distribution of absorbed dose of light radiation applying numerical Monte-Carlo simulations for multilayer media mimicking biotissues and the analysis of the effect of biotissue optical properties on this distribution.

The aim of the study is to develop approaches for fluorescence monitoring and planning of photodynamic therapy employing chlorine series photosensitizers.

Materials and Methods. The study was performed for chlorine series PS Photoditazin (Veta Grand, Russia). The experimental part of the work included the study of the fluorescence imaging potential in the estimation of PS penetration depth into the biotissue both on phantoms and on human skin in vivo.

Experiments with biotissue phantoms. The model experiment was performed with agar phantoms of biotissue prepared from water, intralipid 20%, and red and black inks. Components concentrations were chosen to ensure that the optical properties of the phantom at wavelengths of 405 and 660 nm corresponded to typical biotissue optical properties of [19]. The recording of fluorescence images was performed with a custom-built device for PDT monitoring developed by our group [20]. This device was improved to allow for two-wavelength excitation of the PS by adding a LED source at 405±10 nm synchronized with the camera in addition to the 660±10 nm source.

PS concentration in a phantom was 0.05 mg/ml while the initial one in delivery package was 5.0 mg/ml. PS was uniformly distributed within the volume of the upper phantom layer which thickness d varied from 0.25 to 6 mm. The lower layer of the phantom did not contain PS, and total thickness of the phantom equaled 6 mm (Figure 2).

Figure 2. The schematic of agar biotissue phantom:

µ_a — medium absorption coefficient, µ_s — medium scattering coefficient, g — anisotropy factor, µ^ps_a — photosensitizer absorption coefficient, d — thickness of the layer containing photosensitizer

In vivo experiment. Pilot in vivo experiment was carried out on the skin of the forearm inner side of a healthy female volunteer (41 years). The study was conducted in accordance with Protocol No.7 of the meeting of the local Ethics Committee of the Nizhny Novgorod State Medical Academy on conducting research with human subjects (July 3, 2017). PS Photoditazin was topically applied to skin surface in a volume of 100 μl with subsequent uniform distribution over an area of 24 cm². After the application, the site with the applied PS was monitored for 5 min using a PDT device. The position of the volunteer’s hand was fixed during the entire monitoring time.

Estimation of PS penetration depth. Estimation of PS penetration depth was carried out using the approach previously proposed in [17, 18]. It is based on the development of numerical model for fluorescent response of biological tissue in the presence of PS. The model is based on the calculation of the distribution of probing radiation S_ex at the excitation wavelength λ_ex within the tissue basing on the radiative transfer theory and the subsequent calculation of the fluorescence response S_em, when the emission map corresponding to fluorescence wavelength λ_em is calculated on the basis of the absorption map of exciting radiation.

It is proposed to use the ratio of fluorescent signals, corresponding to the wavelengths λ_ex=405 nm and λ_ex=660 nm respectively, as a parameter which characterizes PS penetration depth. In model and in vivo experiments fluorescent signal is calculated as the mean over the area of PS application.

Simulation of fluorescent response and the spatial distribution of the radiant exposure and the absorbed dose was performed applying Monte-Carlo technique. It is a statistical simulation technique based on the simulation of a large number of random photon trajectories in a medium, based on the specified optical properties and the irradiation geometry, and the subsequent statistical analysis of the obtained data. In this paper we used an algorithm previously developed in [21–23].

Fluorescent response modeling. In course of Monte-Carlo simulations, fluorescent responses were obtained for phantoms containing Photoditazin with concentration of 0.05 mg/ml and 0.5 mg/ml uniformly distributed in the upper layer with varied thickness which corresponded to the geometry of model experiments with phantoms. Optical properties of the model tissue corresponded to those typical for biological tissues [19]. Optical properties of the medium and PS absorption coefficient are shown in Table 1.

Table 1. Optical properties of the model tissue and photosensitizer absorption coefficient

The model medium with dimensions of 20×20×6 mm³ was considered to be uniformly irradiated over the entire surface. The PS penetration depth into the medium varied from 0.25 to 6 mm, the boundary between the layers containing and not containing PS was considered to be sharp.

Numerical simulation of radiant exposure and absorbed dose distribution. Monte-Carlo simulation of the distribution of absorbed radiation dose was performed for a planar geometry sample with the thickness of 4 mm and transverse dimensions of 10×10 mm². It was assumed that the sample surface was uniformly illuminated by radiation at one of the specified wavelengths (405 and 660 nm) with a total light dose of 50 J/cm².

Human skin was considered as a model object. In this study a simplified three-layer skin model was considered, consisting of stratum corneum (50 μm thick), epidermis (150 μm), and dermis (3.8 mm) layers. All the layers were considered to be optically homogeneous; the optical properties of the layers at the considered wavelengths are displayed in Table 2. Refractive index for all three layers was considered to be 1.4.

Table 2. Optical properties and thickness of skin layers employed in numerical simulation [15, 16, 24]

In the frames of this study the Monte-Carlo algorithm was adapted for MATLAB environment. Algorithm implementation in MATLAB environment is based on simultaneous processing of 10⁶ photon trajectories. Firstly, photon parameters, such as the initial position in Cartesian coordinates, the propagation direction, and the initial weight W, are initialized. These characteristics are stored as arrays, where each line corresponds to a single photon and the total number of lines is equal to the total number of photons. Then the data sets are processed in accordance with Monte-Carlo algorithm, which takes into account changes in the photon trajectory due to scattering and the decrease in the photon weight due to absorption in tissues.

In this case we understand the absorbed dose of the radiation in the medium elementary volume as the total weight that photons lost due to absorption in a given elementary volume. Elementary volume is a cube of 0.05×0.05×0.05 mm³.

Results

Photosensitizer penetration monitoring by fluorescence imaging

Numerical simulation and model experiment. Since PSs are fluorescent markers, fluorescence imaging is the most obvious approach to optical monitoring of PDT, and two absorption peaks in chlorine series PS spectra provide additional opportunities for monitoring the presence of a PS in tissues. The comparison of the results of numerical simulation and the model experiment on measuring the ratio of fluorescence signals after excitation at the wavelengths of 405 and 660 nm is shown in Figure 3.

Figure 3. Ratio of fluorescent signals after excitation at λ_ex=405 nm and λ_ex=660 nm, calculated with Monte-Carlo simulation and measured in model experiment; photosensitizer concentration was 0.05 mg/ml

Since biotissues absorption coefficient for λ_ex=405 nm is much higher than that for λ_ex=660 nm, absorption at λ_ex=405 nm occurs predominantly in the superficial layers of biotissue, while for λ_ex=660 nm absorption occurs in the deeper layers, therefore the ratio S_λ_{=405 nm}/S_λ_{=660 nm} monotonically decreases with the increase of the thickness of PS-containing layer. Quantitative comparison of absorbed dose at various depths in biotissue for λ_ex=405 nm and λ_ex=660 nm will be demonstrated below. There is a good agreement between model experiment and numerical model, which suggests that measuring signals ratio at these two wavelengths can serve as an effective indicator of PS penetration depth, however, it should be noted that in order to apply this approach correctly, it is necessary to know optical properties of the inspected biotissue.

In vivo experiment. Pilot in vivo experiment was performed on human skin to test this hypothesis. Typical fluorescent images for excitation at the wavelengths of λ_ex=405 nm and λ_ex=660 nm are shown in Figure 4.

Figure 4. Typical fluorescent images for excitation at λ_ex=405 nm (a) and λ_ex=660 nm (b)

The results of monitoring PS penetration into human skin (inner side of forearm, healthy female volunteer, 41 years) after topical application are shown in Figure 5. As was shown above in the model experiment, the ratio of the fluorescent signals falls with penetration depth increase, which agrees well with the dynamics observed in course of in vivo experiment. For qualitative comparison, Figure 5 also shows numerical simulation results for two concentrations of PS, 0.05 and 0.5 mg/ml. It should also be noted that in case of topical PS application, PS distribution within tissue volume differs from the uniform distribution considered in numerical simulation and model experiment [25]. According to estimations (the ratio of quantity of applied PS and the application area), the concentration of PS in the volunteer’s skin was about 0.1–0.2 mg/ml. In addition, it must be taken into account that the optical properties of the volunteer’s skin may differ from the optical properties of the phantom. Considering all of abovementioned, we can say that the results of in vivo experiments are consistent with the results of the model experiment and numerical simulation, and model curves can be used to estimate PS penetration depth in human skin. PS accumulation in human skin was confirmed by the results of fluorescence imaging at 24 and 48 h after in vivo experiment.

Figure 5. Ratio of fluorescent signals after excitation at λ_ex=405 nm and λ_ex=660 nm, calculated with Monte-Carlo simulations for photosensitizer concentrations of 0.5 mg/ml and 0.05 mg/ml, and dynamics of the ratio of fluorescent signals obtained in course of in vivo experiment with photosensitizer Photoditazin

Thus we have shown that the ratio of fluorescent signals for different PS excitation wavelengths can serve as a tool for differentiating the depth of PS penetration up to 1.5–2.0 mm (the limit depends on optical properties of the tissue and the concentration of accumulated PS). The latter limitation is associated with limited light penetration into biological tissues.

PDT planning with Monte-Carlo simulation

Calculation of distributions of radiant exposure and absorbed light dose. One of the factors determining the efficiency of a PDT procedure is the distribution of absorbed radiation in biological tissue, the so-called light dose. Thus, an important step in PDT planning is to study the propagation of radiation in inhomogeneous media and to estimate the volumetric distribution of the absorbed fraction of radiation. The most promising approach for solving these problems is numerical simulation employing Monte-Carlo technique.

During the study, maps of radiant exposure and absorbed light dose in a model multilayer sample mimicking structure of human skin were calculated by Monte-Carlo technique for illumination at 405 and 660 nm (Figures 6 and 7, respectively), while the light dose on the surface of the tissue equaled 50 J/cm² (0.5 J/mm²). The presented maps allow estimating the in-depth distribution of radiant exposure and absorbed dose. It should be noted that during PDT planning absorbed dose is of significant importance, since it characterizes the intensity of photodynamic reaction. From the presented dependences one can see that for 405 nm, the main photodynamic effect will be observed in tissue at depths of up to 0.5 mm, while for 660 nm this value will be about 2 mm.

Figure 6. Distribution maps of (а) radiant exposure (the color scale shows the value in J/mm²) and (b) absorbed light dose (the color scale shows the value in J/mm³) for λ_ex=405 nm

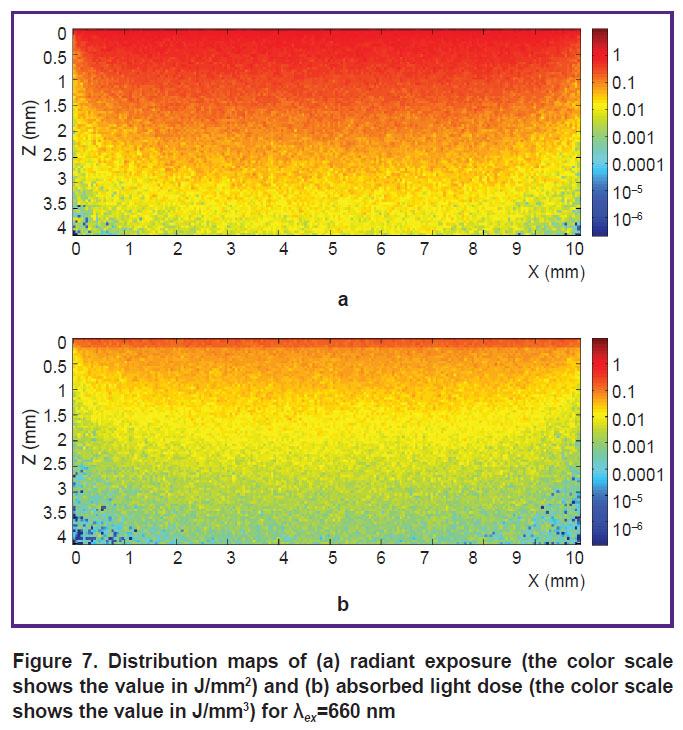
Figure 7. Distribution maps of (а) radiant exposure (the color scale shows the value in J/mm²) and (b) absorbed light dose (the color scale shows the value in J/mm³) for λ_ex=660 nm

Effect of optical properties on absorbed light dose distribution. To study the effect of tissue optical properties variation on absorbed light dose distribution we performed Monte-Carlo simulations of this distribution for a three-layer medium with optical parameters corresponding to those of human skin at 405 and 660 nm (see Table 1), however, the absorption and scattering coefficients were separately varied within the range of ±60% from the basic values.

Figure 8 (a) and Figure 9 (a) show the comparison of absorbed light dose at three different depths (0.1, 0.5, and 1 mm) for different absorption coefficients of model tissue and fixed scattering coefficient in the case of illuminating the sample at 405 and 660 nm, respectively. At 405 nm, absorption coefficient of stratum corneum (the thickness of which equals 0.05 mm in the model) significantly exceeds absorption coefficients of underlying layers. Thus, the photon undergoes a significant loss of weight passing through stratum corneum (see Figure 8 (a)). This trend is also maintained for variation in the value of absorption coefficient in model tissue layers. However, decrease in absorption coefficient leads to decrease in the fraction of photons weight loss at small depths and to increase in absorbed light dose at large depths.

Figure 8. Comparison of absorbed light dose at three depths for ±30 and ±60% variations of (a) absorption coefficient and (b) scattering coefficient in the case of sample illumination at λ_ex=405 nm

Figure 9. Comparison of absorbed light dose at three typical depths for ±30 and ±60% variations of (a) absorption coefficient and (b) scattering coefficient in the case of sample illumination at λ_ex=660 nm

In the case of layers absorption coefficients variations for 660 nm (see Figure 9 (a)), at the depths of 0.1 and 0.5 mm, the largest absorbed light dose corresponds to basic values, and its value decreases both for increase and decrease in absorption coefficient. Two effects compete here: the abovementioned effect when absorption increase in the upper layers causes smaller amount of radiation reaching large depths and being absorbed there and the effect of absorbed dose decrease due to direct reduction of absorption coefficient.

Figure 8 (b) and Figure 9 (b) demonstrate similar comparison of absorbed light dose at three different depths when scattering coefficient of model tissue is varied while the absorption coefficient is kept fixed. For the fixed absorption coefficient, the magnitude of the light dose at all three depths increases with the decrease in tissue scattering coefficient. Indeed, propagating in tissues with larger scattering coefficient, photons need to travel longer path in order to reach certain depth due to substantial multiple scattering, which causes significant decrease in their weight due to absorption yet at smaller depths.

Thus, it is demonstrated that PDT requires taking into account the distribution of both radiant exposure and absorbed light dose; moreover, for the same incident dose these distributions essentially depend on the radiation wavelength and on the local optical properties of biotissue. Numerical Monte-Carlo simulations allow to more accurately estimate the distribution of incident light energy in biological tissues, moreover, in particular cases the dependence on optical properties is nonlinear.

Discussion. In order to increase the efficiency of PDT procedure it is necessary to control PS distribution and photobleaching in tissue, as well as to know the distribution of optical radiation. Since PSs are fluorescent markers, the control of PS distribution and photobleaching can be performed with optical imaging techniques, while numerical simulation of radiation propagation in inhomogeneous media can be used to estimate the distribution of light dose within the tissue.

In this paper we discuss approaches to monitoring PS penetration into tissue after topical application by fluorescence imaging technique and estimating the distribution of light dose in biological tissues using numerical Monte-Carlo simulations.

It is shown that the ratio of fluorescent signals detected after excitation at 405 nm and 660 nm can be used to evaluate the dynamics of chlorine series PS penetration into tissue. Monotonic decrease in this ratio with increase in penetration depth is shown in numerical simulation and in model experiment. The results are in good agreement with the results of pilot in vivo experiment in which the signal ratio decreases monotonically with time.

By means of Monte-Carlo numerical simulations of the distribution of absorbed light dose in a simplified three-layer model of human skin a significant dependence of absorbed light dose on local optical properties of tissue is revealed at characteristic depths of 0.1, 0.5, and 1 mm. It should be noted that this dependence has difference for the considered wavelengths of 405 and 660 nm. In particular, for 405 nm, with an increase in the absorption and scattering coefficients of the model tissue layers, the fraction of absorbed radiation is reduced monotonously at all three depths under consideration for the same incident light dose. However, for variations of tissue optical properties corresponding to 660 nm, at small depths the largest absorbed light dose corresponds to the basic values, and its value decreases both with increase and decrease in absorption coefficient. The variation of optical properties in real biological tissues can reach up to 30%, so taking into account individual characteristics and estimating the distribution of absorbed light dose in numerical simulations by Monte-Carlo method with subsequent correction of PDT procedure can significantly improve its efficiency.

Acknowledgements. The authors are grateful to N.M. Shakhova, V.I. Plekhanov and S.V. Gamayunov for useful discussions.

Funding. The work is supported by Russian Science Foundation (project #17-15-01264).

Conflict of Interests. The authors have no conflict of interests to disclose.

References

Allison R.R., Moghissi K. Photodynamic therapy (PDT): PDT mechanisms. Clin Endosc 2013; 46(1): 24–29, https://doi.org/10.5946/ce.2013.46.1.24.
Akopov A.L., Kazakov N.V., Rusanov A.A., Karlson A. The mechanisms of photodynamic action for treating of cancer patients. Biomedical Photonics 2015; 4(2): 9–16.
Allison R.R., Moghissi K. Oncologic photodynamic therapy: clinical strategies that modulate mechanisms of action. Photodiagnosis Photodyn Ther 2013; 10(4): 331–341, https://doi.org/10.1016/j.pdpdt.2013.03.011.
Filonenko E.V., Serova L.G. Photodynamic therapy in clinical practice. Biomedical Photonics 2016; 5(2): 26–37.
Juarranz A., Jaén P., Sanz-Rodríguez F., Cuevas J., González S. Photodynamic therapy of cancer. Basic principles and applications. Clin Transl Oncol 2008; 10(3): 148–154, https://doi.org/10.1007/s12094-008-0172-2.
Kharkwal G.B., Sharma S.K., Huang Y.Y., Dai T., Hamblin M.R. Photodynamic therapy for infections: clinical applications. Lasers Surg Med 2011; 43(7): 755–767, https://doi.org/10.1002/lsm.21080.
Biel M.A. Photodynamic therapy of head and neck cancers. Methods Mol Biol 2010; 635: 281–293, https://doi.org/10.1007/978-1-60761-697-9_18.
Plaetzer K., Krammer B., Berlanda J., Berr F., Kiesslich T. Photophysics and photochemistry of photodynamic therapy: fundamental aspects. Lasers Med Sci 2009; 24(2): 259–268, https://doi.org/10.1007/s10103-008-0539-1.
Allison R.R. Future PDT. Photodiagnosis Photodyn Ther 2009; 6(3–4): 231–234, https://doi.org/10.1016/j.pdpdt.2009.10.003.
Celli J.P., Spring B.Q., Rizvi I., Evans C.L., Samkoe K.S., Verma S., Pogue B.W., Hasan T. Imaging and photodynamic therapy: mechanisms, monitoring, and optimization. Chem Rev 2010; 110(5): 2795–2838, https://doi.org/10.1021/cr900300p.
Fei B., Wang H., Wu C., Chiu S.M. Choline PET for monitoring early tumor response to photodynamic therapy. J Nucl Med 2010; 51(1): 130–138, https://doi.org/10.2967/jnumed.109.067579.
Wang H., Fei B. Diffusion-weighted MRI for monitoring tumor response to photodynamic therapy. J Magn Reson Imaging 2010; 32(2): 409–417, https://doi.org/10.1002/jmri.22247.
Jo J., Lee C.H., Kopelman R., Wang X. Lifetime-resolved photoacoustic (LPA) spectroscopy for monitoring oxygen change and photodynamic therapy (PDT). Proc SPIE Int Soc Opt Eng 2016; 9708: 97081L, https://doi.org/10.1117/12.2213083.
Gamayunov S., Turchin I., Fiks I., Korchagina K., Kleshnin M., Shakhova N. Fluorescence imaging for photodynamic therapy of non-melanoma skin malignancies — a retrospective clinical study. Photonics & Lasers in Medicine 2016; 5(2), https://doi.org/10.1515/plm-2015-0042.
Salomatina E., Jiang B., Novak J., Yaroslavsky A.N. Optical properties of normal and cancerous human skin in the visible and near-infrared spectral range. J Biomed Opt 2006; 11(6): 064026, https://doi.org/10.1117/1.2398928.
Tuchin V.V. Lazery i volokonnaya optika v biomeditsinskikh issledovaniyakh [Lasers and fiber optics in biomedical research]. Moscow: FIZMALIT; 2010.
Swartling J., Bengtsson D., Terike K., Svensson J., Andersson-Engels S. Estimation of depth of fluorescing lesions in tissue from changes in fluorescence spectra. Optical Tomography and Spectroscopy of Tissue VI 2005; 5693: 225–231, https://doi.org/10.1117/12.590145.
Swartling J., Svensson J., Bengtsson D., Terike K., Andersson-Engels S. Fluorescence spectra provide information on the depth of fluorescent lesions in tissue. Appl Opt 2005; 44(10): 1934–1941, https://doi.org/10.1364/ao.44.001934.
Loginova D.A., Sergeeva E.A., Krainov A.D., Agrba P.D., Kirillin M.Yu. Liquid optical phantoms mimicking spectral characteristics of laboratory mouse biotissues. Quantum Electronics 2016; 46(6): 528–533, https://doi.org/10.1070/qel16133.
Kleshnin M.S., Fiks I.I., Plekhanov V.I., Gamayunov S.V., Turchin I.V. Compact and fully automated system for monitoring photodynamic therapy, based on two LEDs and a single CCD. Laser Phys Lett 2015; 12(11): 115602, https://doi.org/10.1088/1612-2011/12/11/115602.
Kirillin M., Perekatova V., Turchin I., Subochev P. Fluence compensation in raster-scan optoacoustic angiography. Photoacoustics 2017; 8: 59–67, https://doi.org/10.1016/j.pacs.2017.09.004.
Loginova D.A., Sergeeva E.A., Fiks I.I., Kirillin M.Yu. Probing depth in diffuse optical spectroscopy and structured illumination imaging: a Monte Carlo study. Journal of Biomedical Photonics & Engineering 2017; 3(1): 010303, https://doi.org/10.18287/jbpe17.03.010303.
Kirillin M.Yu., Farhat G., Sergeeva E.A., Kolios M.C., Vitkin A. Speckle statistics in OCT images: Monte Carlo simulations and experimental studies. Opt Lett 2014; 39(12): 3472–3475, https://doi.org/10.1364/ol.39.003472.
Patwardhan S.V., Dhawan A.P., Relue P.A. Monte Carlo simulation of light-tissue interaction: three-dimensional simulation for trans-illumination-based imaging of skin lesions. IEEE Trans Biomed Eng 2005; 52(7): 1227–1236, https://doi.org/10.1109/tbme.2005.847546.
Lopez N., Mulet R., Rodríguez R. Tumor reactive ringlet oxygen approach for Monte Carlo modeling of photodynamic therapy dosimetry. J Photochem Photobiol B 2016; 160: 383–391, https://doi.org/10.1016/j.jphotobiol.2016.04.014.