Nanoscale Modeling of Morphological Disordering of Mineral Matrix Elements

Semenov А.S., Grishchenko А.I., Melnikov B.E.

Key words: bone tissue biomechanics; nanocomposite; homogenization; elasticity; strength; disordering of conglomerates; intercrystalline bridge; finite element method.

The aim of the investigation was to develop a nanoscale functional model of bone matrix by combining its mineral elements into a single structure of mineral compounds, analyze the axial disorder effect of its elements on the effective elastic modules, and the distribution of stress-strain fields in a modeling structure using a finite element technique.

Materials and Methods. We proposed a new morphological nanoscale model of bone tissue (at the level of collagen fibrils) taking into account the mineral bridges between the bonds of hydroxyapatite crystals based on Denisov-Nikolsky’s model. We analyzed the effect of variation of morphological characteristics on local stress-strain state and mechanical properties of the representative bone volume element by means of the direct finite element simulation and homogenization.

Results. The increase of minerals disorder degree was found to be accompanied by the increase of strain and stress in a modeled structure. An elastic modulus value is slightly affected by disordering. The biological relevance of the phenomenon is in that the mineral disorder, regardless of the force direction, always increases the risk of bone matrix damage.

Conclusion. We developed a nanoscale functional model of bone matrix by combining its mineral elements into a single structure using mineral compounds. We determined the impact of axial disordering of it elements on effective elastic modules, and the distribution of stress-strain fields in a modeling structure using a finite element technique. The analysis of the results showed the qualitative relationship of the findings with the experiment.

Modern diagnostic techniques based on atomic force microscopy [1–3] enable to study the nanoscale morphology and mechanical properties of bone tissues; however, they have a number of limitations, in particular, due to the fact that only a surface layer of a sample can be studied. The study of computerized simulation methods in addition to direct objective methods enables to obtain the data on the processes inside the volume, as well as investigate the effect of a microstructure on mechanical properties of bone tissues by carrying out multi-variant simulation experiments. Osteologic computer models allow determining variables that influence biosystem response results achieved at lower costs and time expenditures [4].

However, it should not be overlooked that for computerized simulation we use simplified patterns of an object under study, and the correctness of results is determined by structure-functional model adequacy. In our case a simplified pattern should show the main nanoscale morphofunctional characteristics of bone tissue. A morphological constitutive bone matrix model put forward by Denisov-Nikolsky et al. [3] was chosen as a prototype, since compared to other models it relies on the presence of intercrystalline bridges, which have an effect on mechanical properties of bone tissue [5].

The model exhibits the following characteristics [3, 6, 7]. Minerals are arranged in the basic substance outside and inside the fibrils (Figure 1). In interfibrillar spaces the assembling of crystallites adjacent to collagen fibrils surround them forming cuffs and contact with intrafibrillar assemblings. At a distance from collagen fibrils, crystallites form conglomerates, in which they are facing one direction. Relative to each other, these conglomerates are situated at different angles. Intrafibrillar crystalline assembling form a row of parallel helically-coiled layers oriented at 8–25° to fibril axis. Separate mineral assemblings bind the adjoining layers providing mineral element continuity of fibrils after organic constituent removal.

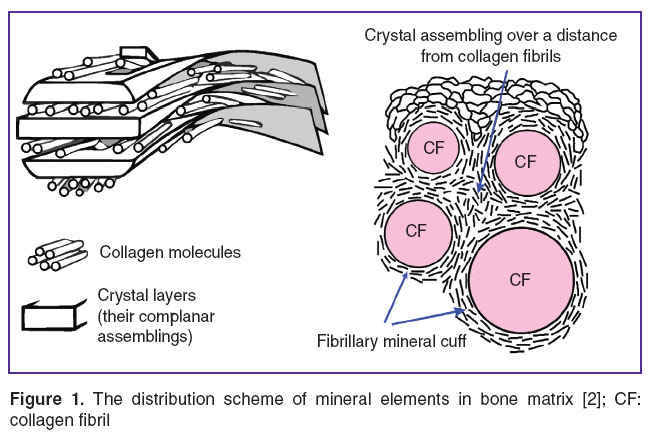Figure 1. The distribution scheme of mineral elements in bone matrix [2]; CF: collagen fibril

Among the mentioned morphological characteristics of bone matrix we have distinguished two essential ones: 1) mineral spatial ordering along their X-axes in relation to X-axis of fibrils, and 2) the presence of mineral bonds between them, the bonds forming a single mineral array in every bone. It will allow assessing biologically the role of organic matrix and it relationships with mineral matrix.

Structural order of mineral matrix depends on organic order, since the latter initiates mineral nucleation and determines their directed growth, and by that determining its three-dimensional organization [8]. In other words, mineral matrix in every bone tissue locus is programmed reflection of organic matrix ultrastructure. Therefore, the more optimal three-dimensional organization of the latter in relation to dominating directions of constant mechanical loading, the more optimal mechanical properties of bone structures in every skeletal part.

One of the main reasons for variations on organic matrix structure are neurohumoral changes in the body resulted from acute diseases, extreme factors (surgeries, neuro-emotional stimulus, etc.), chronic diseases, ageing, etc. The alterations of bone matrix structures being formed are adaptive, and in fact, similar to those occurring in blood, though unlike them they are stable structurally. In the course of remodeling the variations gradually accumulate [9], and it is our opinion that it is manifested in the change of axial conjugacy of mineral matrix elements observed as the body ages [10]. It is due to the fact that when ageing there is the collagen denaturation in the course of organic matrix formation in response to enzymes, i.e., breaking and uncoiling of triple helical structure of molecules. Moreover, the bond and geometry character of collagen fibrils and fibers also changes, there has been growing the number of collagen cross linkages and fiber orientation deviation. Such changes are accompanied by the decrease of bone structure strength limit, which is significantly lower at ageing [11–14]. It indicates why the assessment of the disordering degree effect of mineral structures on mechanical properties of bone matrix is one of the critical pathogenic tasks the solution of which will enable to comprehend nanoscale initiation mechanisms of fatigue damages resulting in low-energy fractures.

Mineral bonds between minerals [3, 5–7] unite mineral matrix in a unified complex in every bone and make us view from a new angle the role of organic and mineral constituents in the formation of mechanical properties of bone structures. The consideration of the bonds is a substantial addition to current dominant concepts, which ignore their existence. According to one of the concepts [15], collagen prevents bone structures from damaging under tension, and collagen — under compression. In accordance with another concept [16], bone is a two-component composite, of collagen matrix type with unbound mineral inclusions.

Materials and Methods

General characteristics of a computing morphofunctional model. To assess the effect of structural disordering of mineral matrix on strength and rigidity, within a framework of the model suggested by Denisov-Nikolsky et al. [3], in calculations we used its simplified version: representative volume element (RVE) of the material, minimal volume containing a priori all statistic information related to the distribution and morphology of nanoscale material irregularities. Crystalline assemblings in RVE have a staggered arrangement, and represent a single mineral block, since they are connected with each other by mineral bridges.

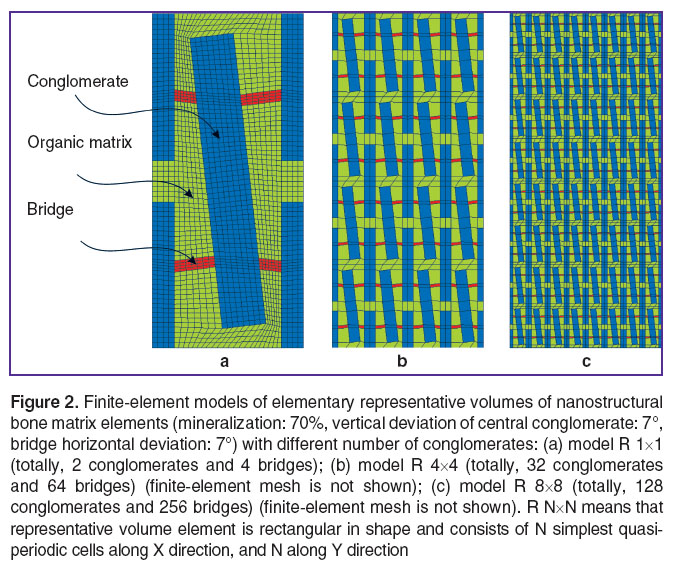
The simplest RVE version (a quasi-periodicity cell) (Figure 2 (а)), schematically interpreting nano-inhomogeneity, has a central crystalline conglomerate deviated from vertical direction and four fragments of neighbor undeviated minerals (1/4 of each mineral area) with four bridges between them and a central mineral. Further consideration of possible mutual disordering of conglomerates and bridges, random distribution of orientations, locations of centers and sizes require consideration of RVE containing a large number of conglomerates (Figure 2 (b), (c)). An increased number of conglomerates in RVE along with the expansion of opportunities to consider bone tissue microstructure irregularities enables to predict effective mechanical properties more precisely, since the effect of external boundaries is diminished.

Figure 2. Finite-element models of elementary representative volumes of nanostructural bone matrix elements (mineralization: 70%, vertical deviation of central conglomerate: 7°, bridge horizontal deviation: 7°) with different number of conglomerates: (а) model R 1×1 (totally, 2 conglomerates and 4 bridges); (b) model R 4×4 (totally, 32 conglomerates and 64 bridges) (finite-element mesh is not shown); (c) model R 8×8 (totally, 128 conglomerates and 256 bridges) (finite-element mesh is not shown). R N×N means that representative volume element is rectangular in shape and consists of N simplest quasi-periodic cells along X direction, and N along Y direction

The described model [3] was implemented in the finite element program PANTOCRATOR [17]. A finite element method in elasticity theory is introduced based on the equation of virtual work. The numerical solutions of partial differential equilibrium equations are obtained by potential energy minimization reducing the task to the search for solving a system of linear algebraic equations. PANTOCRATOR enables to generate automatically discrete RVE models of arbitrary geometry, solve elastic boundary value problems, and determine effective elastic moduli and strength properties of RVE, analyze the distribution of stress-strain fields for nanoscale morphological structure of a matrix fragment. When solving boundary problems, equilibrium configurations of heterogeneous medium RVE are studied based on the principle of momentum conservation and the principle of angular momentum conservation.

Key parameters of the finite-element model of RVE of bone tissue nanocomposite.

1. The task is solved under the assumption of plane strain state. RVE model is rectangular in shape (See Figure 2). The comparison of the three-dimensional solution with two-dimensional solution showed acceptable accuracy of plane strain formulation for considered parameters of a stress state.

2. Mineral conglomerates in RVE model are also rectangular in shape (See Figure 2), since it corresponds to an average shape of a crystallite [18] and coplanar assemblings [3], as well as enables to use simple finite-element models to perform computations when forming RVE.

3. The dimensions of every crystalline assembling along the principle axes are 2,500×350 nm. The dimensions of mineral bridges vary depending on their orientation and the crystallite orientation, their average size is 200×30 nm; total weight content of mineral component in RVE is 70% (corresponds to 55% RVE area) that is common with mature bone tissue. The mentioned dimensions of minerals comply with the sizes of calcospherites described by Boyde [19, 20] in forming bone parts. Considering that in mineralizing bone matrix in adults the distances between fibrils do not exceed 20–30 nm, morphological mineral substrate includes the fragments of mineralized collagen fibrils (50–80 nm in diameter and up to 2,000 nm in length) with surrounding cuffs, single matrix vesicles (30–200 nm in diameter), and differently directed crystal groups binding the cuffs of adjacent fibrils.

4. Crystallite assemblings have a staggered arrangement, and embedded in organic matrix. There is only one bridge between every pair of adjacent crystallite assembling.

5. In the model under discussion one should consider the presence of vertical deviation of mineral axes, and bridge axes deviated from horizontal axes. The angle of mineral axes deviation characterizing the disordering degree was assigned deterministically, and varied within the range from 0 to 8°. The angles of bridge deviation from normals to conglomerates varied from –45 to 45°.

6. RVE is a heterogeneous three-component material (mineral conglomerates, mineral bridges and organic matrix); boundary value problems of determining stress-strain state of RVE are solved within framework of the linear elastic formulation.

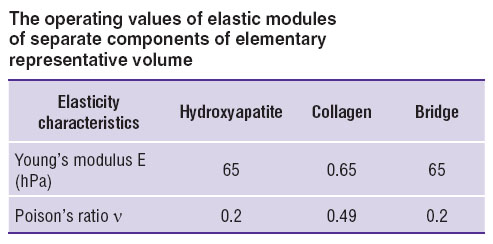
7. Mechanical properties of separate components of the model were taken as those corresponding to isotropic materials, the values of nanoscale elastic moduli were borrowed from literature [18–20] (See the Table).

The operating values of elastic modules of separate components of elementary representative volume

Assessment of effective elastic properties based on finite-element analysis. Submicroscopically, effective properties of bone tissue were taken as those corresponding to orthotropic elastic material; and Hooke’s law can be presented as follows:

where 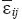is strain tensor; 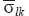is stress tensor; 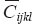is elastic compliance tensor of 4^th rank. The bar over the introduced tensors means the conformance to homogeneous (mean) material. The characteristics of separate components of heterogeneous material are indicated with out a bar. A symmetric matrix of elastic compliances 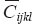corresponds to tensor [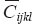] in its own anisotropic axes for orthotropic material, the matrix having the following structure:

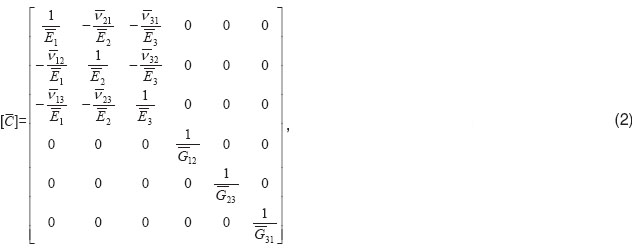
where 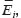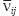and 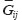are Young’s modules, Poison’s ratios, and shearing modules of elasticity (i, j = 1, 2, 3), for their determination we solved a series of boundary problems with various boundary conditions corresponding to RVE loading in different directions. The determined constants of homogenized material should provide the energy equality when homogenized and heterogeneous RVE material is deformed. To calculate the matrix components of effective elastic compliances 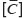(2) we used averaged over representative volume strain-stress tensors obtained in finite-element equations:

To solve a two-dimension (plane strain) problem it is suffices to find four elastic constants: 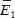, , 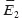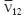and 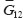. Elastic moduli along the axis orthogonal to RVE plane under consideration can be assessed without loss of accuracy and according to the mixture rule.

Results and Discussion. When carrying out the investigation the following problems were solved sequentially:

1) electron microscopic confirmation of morphological disordering of mineral bounds between minerals and between minerals themselves under pathological conditions, or at ageing compared to the norm;

2) the assessment of the effect of mineral oblique angle of main mineral axes in relation to the major RVE axes (disordering degree) on mechanical properties of bone matrix;

3) the assessment of the effect of deviation of the main axes of mineral bridges from horizontal direction on mechanical properties of bone matrix.

Morphological disordering of mineral bonds between minerals and between minerals themselves under pathological conditions, or at ageing compared to the norm has its confirmation in literature reports [21]. The disordering causes were considered above.

The effect of mineral deflection angles. To assess the effect of mineral disordering angle in RVE on its stress-strain state and effective elastic properties, we performed finite-element computations with three different angles: 0, 4 and 8°. Larger deflection angles for geometric parameters under consideration cannot be managed to reach due to the limited contact of the conglomerate to be turned and the adjacent unturned minerals (Figure 3). The results of computing experiments carried out with RVE from R 1×1 to R 8×8 (R N×N means that RVE is rectangular in shape, and consists of N elementary quasiperiodicity cells along X-axis and N along Y-axis) demonstrated that the turn of just one conglomerate hardly has an effect on the values of effective elastic moduli 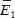, 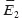(the differences are less than 1%), though influences the maximum stress intensity level (Figure 4), which determines the local damage possibility. When a conglomerate is turned by 8° angle, the maximum stress intensity when subjected to rigid loading (mechanical action under the conditions of prescribed displacements, or a strain tensor component) in vertical direction increases by 36%, and by 18% when loaded in horizontal direction compared to the corresponding idealized version without orientation deviation. When subjected to soft loading (mechanical action under the conditions of prescribed external forces, or a stress tensor component) the effect of increasing stress intensity effect when a conglomerate is turned has the same order, and amounts 31 and 26%, respectively.

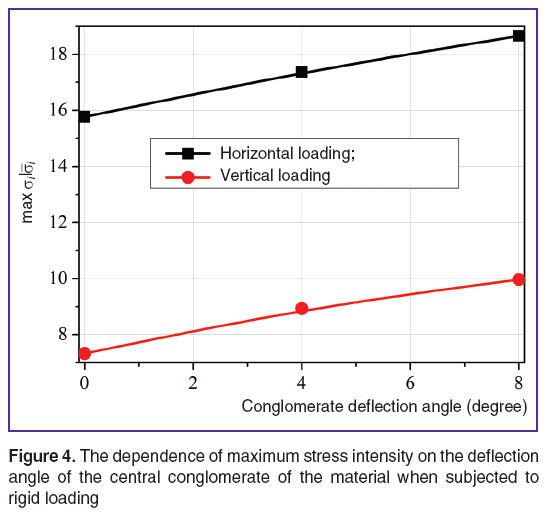Figure 3. The distribution of stress intensity in a fragment of elementary representative volume of the material with 4° (a) and 8° (b) turn of a singular conglomerate when subjected to soft loading in vertical direction

Figure 4. The dependence of maximum stress intensity on the deflection angle of the central conglomerate of the material when subjected to rigid loading

When calculating maximal strain values in angular singular bridge points we used locally averaged values in the range of one finite element, its typical size being 5 nm. It should be noted that the process of bridge failure is defined by integral stress state within the elementary structural constituent element, and therefore it is locally averaged stress values that are most informative when bridge strength is assessed. The selection of local averaged area requires further detailed study.

Based on the above mentioned we can conclude that disordering of minerals along longitudinal axes in relation to load direction results in bone matrix stress increase. Pathogenically, disordering of mineral conglomerates reduces nanoscale mechanical properties of bone matrix, and therefore, the skeleton in general. Thus, mineral disordering is one of the underlying factors leading to the density increase of fatigue micro-damages of bone tissue, which at ageing grows exponentially in women over forty, and in men over fifty [13, 14].

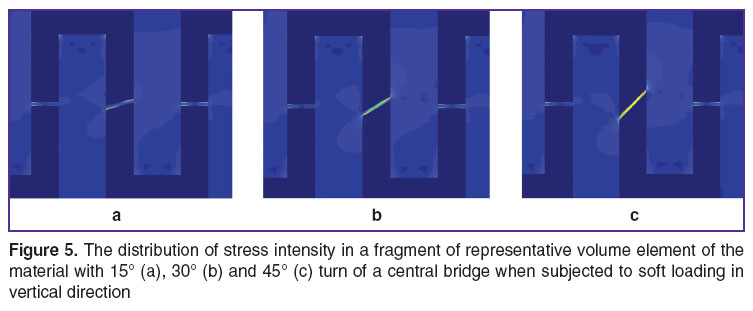
The effect of bridge deflection angles. To assess the effect on stress-strain state and effective RVE elastic properties we performed finite-element computations with various angles deviated from horizontal level: by 15, 30 and 45° (Figure 5). The results of computations using RVE from R 1×1 to R 8×8 showed that the turn of only one bridge has no effect on the values of effective elastic RVE moduli 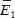, 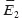(the differences are less than 1%), though has an impact when the stress intensity is maximum (Figure 6).

Figure 5. The distribution of stress intensity in a fragment of representative volume element of the material with 15° (a), 30° (b) and 45° (c) turn of a central bridge when subjected to soft loading in vertical direction

Figure 6. The dependence of maximum stress intensity on bridge horizontal deflection angle when elementary representative volume is subjected to rigid loading — R 1×1 with periodic boundary conditions

The turn of a separate bridge in RVE under some loading conditions was found to increase the extreme stress level in a bridge, while under other conditions it appeared to decrease it. So, if a bridge is deflected through 15° counter-clockwise, the tension in horizontal direction (rigid loading, periodicity conditions) is characterized by the decrease of maximal relative stress intensity by 2%, at 30° — by 12%, at 45° — by 47% compared to the idealized variant without a turn (See Figure 6). This effect is due to the fact that under tension in horizontal direction RVE is shrinked vertically, therefore neighboring conglomerates are displaced vertically relative to each other resulting in the turn of the bridge connecting them, and the appearance of additional stresses in the bridge. Depending on the direction of initial horizontal deflection of a bridge, vertical conglomerate displacements can create additional stress in them (it concerns the bridges, in which the turn under loading compensates the initial turn), as well as additional tension stress (for bridges, in which the turn under loading increases the initial turn).

This script is also realized when subjected to loading in vertical direction, and when 15° deflection of a bridge in the counter-clockwise direction results in the increase of maximal relative stress intensity by 65%, at 30° — by 80%, and at 45° — by 47% compared to the idealized variant without a turn (See Figure 6).

If a bridge is deflected the opposite direction (clockwise) there is more complex non-monotonic dependence of stress intensity on deflection angle (See Figure 6) caused by the change of the point of extreme stress values (Figure 7). Under horizontal tension, the point of maximum stress intensity is moved from the upper part of a bridge to the lower one at deflection angle being under –20°, and under vertical tension, on the contrary, it is moved from the lower part to the upper one at deflection angle being under 0° with a repeated subsequent change of a maximum point from the upper to lower part of a bridge at angles under –38°.

Figure 7. The alteration of maximum strain intensity location (marked with a red triangle) depending on bridge horizontal deviation

Unturned bridge under vertical loading provides minimal values (among all deflection angles) of maximal (at all RVE points) stress intensity (See Figure 6), i.e. is an optimal orientation concerning the local RVE strength. When deflected through 15–30° regardless of the direction, there are local maxima of stress intensity exceeding the value at the point of 0° by 1.5–2 times (See Figure 6). At the same time, an unturned bridge under horizontal loading provides maximum value (among all deflection angles) of maximal (at all RVE points) stress intensity, however, one should take into consideration that the horizontal effect level at standard locomotions is significantly lower that the vertical effect level.

The findings suggest that there are non-optimal directions of mineral bonds in relation to trend directions of mechanical loadings. As a consequence, their fracture risk increases that can be considered as an initial stage of fatigue damage formation. This biomechanical phenomenon is of great pathogenic importance and suggests that in vivo bone matrix “desintegration”, the latter is evident as diffusely stained loci when fatigue damages are histologically revealed [13, 21, 22].

Pathogenically, we should consider that the fracture of separate bridges leads to the increase of load on the rest bridges, and therefore, increases the risk of their subsequent fracture [23]. However, this process under physiological conditions develops relatively slowly, that is why there was suggested continuous hypothetical mechanism to recover fractured connections, which functions if the following conditions are fulfilled [23]:

spatial return of mineral conglomerates into original position existing before the bonds between them had been destroyed due to elastic deformations of bone tissue surrounding the damaged area;

termination of locomotor functions, and therefore the bone structure deformation cease (e.g., during a sleep).

Thus, structural disordering of mineral matrix is due to organic matrix disordering resulted from neurohumoral changes in the body in a number of pathologies and ageing. Nanoscale disordering results in damaging mineral bonds, which are non-optimally oriented in relation to trend directions of mechanical loads, and it is evident at the following hierarchical levels (micro, macro) of structural organization of bone tissue as the decrease of its strength properties and “disintegration”.

Regardless of the mechanical effect direction, as a rule, the higher the degree of mineral disordering, the higher the maximal strain-stress values in a modeled structure, assuming that the elasticity coefficient value undergoes no changes. The phenomenon is of significance, since it presupposes that disordering of minerals irrespective of the direction of effective forces always increases the risk of bone matrix damage.

The data of the study acquired are of apparent biomedical interest, however, they require further detailed model studies including those under the conditions of altered bone matrix mineralization degree, as well as the search for quantitative relationship of the experimental findings in case of disordering effects of mineral matrix elements.

Conclusion. Within the framework of a known morphological model of bone matrix [3] we developed a nanoscale morphofunctional model by combining its mineral elements into a single structure of mineral compounds. Using a finite element technique we determined the axial disorder effect of the structure elements on the effective elastic moduli, and the distribution of stress-strain fields in a modeling structure.

Acknowledgment. The authors express their thanks to A.S. Avrunin, MD, DSc, for fruitful disputes on the problem setting and the discussion of the findings.

Study Funding. The present study was supported by Russian Science Foundation, grant No.15-19-00091.

Conflicts of Interest. The authors declare no conflicts of interest related to the present study.

References

Wallace J.M. Applications of atomic force microscopy for the assessment of nanoscale morphological and mechanical properties of bone. Bone 2012; 50(1): 420–427, http://dx.doi.org/10.1016/j.bone.2011.11.008.
Milovanovic P., Potocnik J., Djonic D., Nikolic S., Zivkovic V., Djuric M., Rakocevic Z. Age-related deterioration in trabecular bone mechanical properties at material level: nanoindentation study of the femoral neck in women by using AFM. Exp Gerontol 2012; 47(2): 154–159, http://dx.doi.org/10.1016/j.exger.2011.11.011.
Denisov-Nikol'skiy Yu.I., Mironov S.P., Omel'yanenko N.P., Matveychuk I.V. Aktual’nye problemy teoreticheskoy i klinicheskoy osteoartrologii [Current problems of theoretical and clinical osteoarthrology]. Moscow: OAO “Tipografiya Novosti”; 2005; 336 p.
Knothe Tate M.L. Multiscale computational engineering of bones: state-of-the-art insights for the future. In: Engineering of functional skeletal tissues. Series title: Topics in bone biology. Vol. 3. Springer London; 2007; p. 141–160, http://dx.doi.org/10.1007/978-1-84628-366-6_10.
Avrunin A.S., Semenov A.S., Fedorov I.V., Mel’nikov B.E., Doctorov A.A., Parshin L.K. Influence of the mineral bond between associations of crystallites on bone matrix mechanical properties. Modeling by the finite element method. Travmatologiya i ortopediya Rossii 2013; 2(68): 72–83.
Doktorov A.A., Denisov-Nikol’skiy Yu.I. Relief features of mineralized surface of lacunes and canaliculi in lamellar bone. Bulleten’ eksperimental’noj biologii i mediciny 1993; 115(1): 61–65.
Zhilkin B.A., Denisov-Nikol’skiy Yu.I., Doktorov A.A. Structure features of lamellar bone of human vertebrae in age involution and osteoporosis. Bulleten’ eksperimental’noj biologii i mediciny 2003; 135(4): 476–480.
Awunin A.S., Tykhylov R.M., Abolin A.B., Shcherbak I.G. Levels of bone mineral matrix organization and the mechanisms determining parameters of its formation. Morfologiya 2005; 127(2): 78–82.
Kornilov N.V., Avrunin A.S. Adaptatsionnye protsessy v organakh skeleta [Adaptive processes in skeletal organs]. Saint Petersburg: MORSAR AV; 2001; 296 p.
Chatterji S., Wall C., Jeffery J. Changes in degree of orientation of bone minerals with age in the human femur. Experientia 1972; 28(2): 156–157, http://dx.doi.org/10.1007/bf01935727.
Wang X., Li X., Shen X., Agrawal С.M. Age-related changes of noncalcified collagen in human cortical bone. Ann Biomed Eng 2003; 31(11): 1365–1371, http://dx.doi.org/10.1114/1.1623488.
Wang X., Puram S. The toughness of cortical bone and its relationship with age. Ann Biomed Eng 2004; 32(1): 123–135, http://dx.doi.org/10.1023/b:abme.0000007797.92559.5e.
Akkus O., Yeni Y.N., Wasserman N. Fracture mechanics of cortical bone tissue: a hierarchical perspective. Crit Rev Biomed Eng 2004; 32(5–6): 379–425, http://dx.doi.org/10.1615/critrevbiomedeng.v32.i56.10.
Akkus O., Adar F., Schaffler M.B. Age-related changes in physicochemical properties of mineral crystals are related to impaired mechanical function of cortical bone. Bone 2004; 34(3): 443–453, http://dx.doi.org/10.1016/j.bone.2003.11.003.
Currey J.D. Three analogies to explain the mechanical properties of bone. Biorheology 1964; 2: 1–10.
Jäger I., Fratzl P. Mineralized collagen fibrils: a mechanical model with a staggered arrangement of mineral particles. Biophys J 2000; 79(4): 1737–1746, http://dx.doi.org/10.1016/S0006-3495(00)76426-5.
Semenov A.S. PANTOCRATOR — konechno-elementnyy programmnyy kompleks, orientirovannyy na reshenie nelineynykh zadach mekhaniki. V kn.: Trudy V mezhdunarodnoy konferentsii “Nauchno-tekhnicheskie problemy prognozirovaniya nadezhnosti i dolgovechnosti konstruktsiy i metody ikh resheniya” [PANTOCRATOR — finite element program complex focused on solving non-linear problems of mechanics. In: Proceedings of V international conference “Scientific and technical problems of prediction of reliability and durability of constructions and the techniques for their solution”]. Saint Petersburg: Izd-vo SPbGPU; 2003; p. 466–480.
N'yuman U., N'yuman M. Mineral’nyy obmen kosti [Bone mineral metabolism]. Moscow: Inostrannaya literatura; 1961; 269 p.
Boyde A., Hobdell M.H. Scanning electron microscopy of lamellar bone. Z Zellforsch Mikrosk Anat 1969; 93(2): 213–231, http://dx.doi.org/10.1007/bf00336690.
Boyde A. Scanning electron microscope studies of bone. In: The biochemistry and physiology of bone. Vol I: Structure. Edited by Bourne G.H. Elsevier BV; 1972; p. 259–310, http://dx.doi.org/10.1016/b978-0-12-119201-3.50015-9.
Fazzalari N.L., Forwood M.R., Manthey B.A., Smith K., Kolesik P. Three-dimensional confocal images of microdamage in cancellous bone. Bone 1998; 23(4): 337–378, http://dx.doi.org/10.1016/s8756-3282(98)00111-2.
Wenzel T.E., Schaffler M.B., Fyhrie D.P. In vivo trabecular microcracks in human vertebral bone. Bone 1996; 19(1): 89–95, http://dx.doi.org/10.1016/8756-3282(96)88871-5.
Avrunin A.S., Tikhilov R.M., Parshin L.K., Melnikov B.E. Hierarchic skeletal organization — a factor regulating the structure of fatigue injuries. Part II. Hypothetical model of formation and distruption of bonds between crystallite associations. Travmatologiya i ortopediya Rossii 2010; 1(55): 48–57.