Усталостная прочность нового биопротеза клапана сердца

Хирургическое протезирование является основной тактикой лечения приобретенных пороков клапанов сердца. Наиболее часто в мировой практике применяют биологические протезы [1, 2], однако по данным международного регистра «Global Valve-in-Valve Registry», большинство имплантированных биопротезов выходят из строя через 9 лет [3, 4]. Развитие вторичной дисфункции обусловливает проведение повторного вмешательства, риск летальности и осложнений которого значительно возрастает [5, 6] за счет увеличения объема операционной травмы — удаления «старого» протеза. Снижение рисков может быть достигнуто путем использования технологии «протез-в-протез» — установки стентоподобного устройства без эксплантации протеза с дисфункцией. В связи с этим разработка конструкции нового протеза клапана сердца для использования в процедуре «протез-в-протез» с бесшовным способом фиксации является актуальной задачей современной кардиохирургии.

Усталостная прочность протезов клапанов сердца является одной из ключевых характеристик, определяющих безопасность и эффективность их применения [7]. Потеря прочности, образование изломов и усталостных трещин при циклическом нагружении способны привести к выходу изделия из строя, возникновению осложнений (тромбообразования, повреждения стенки сосуда, повторного стеноза) или снижению функциональных показателей протеза [8–10]. По российским стандартам требования к циклостойкости протеза — не менее пяти лет функционирования, т.е. 200 млн. циклов «нагрузка-разгрузка», при этом требования FDA к оценке усталости каркаса гораздо строже — 600 млн. циклов [11]. В современном проектировании медицинских изделий на основе пластичных материалов для оценки усталостной прочности широко используют диаграмму Гудмана. Данный подход, базирующийся на физико-механических (одноосное растяжение) и усталостных (S-N-кривая) характеристиках материала, характеризует обе компоненты долговечности — среднее и переменное напряжение в рамках одного эксплуатационного цикла нагружения.

Цель исследования — оценка методом конечных элементов усталостной прочности опорного каркаса разрабатываемого протеза клапана сердца, предназначенного для репротезирования несостоятельного протеза по типу «протез-в-протез».

Материалы и методы

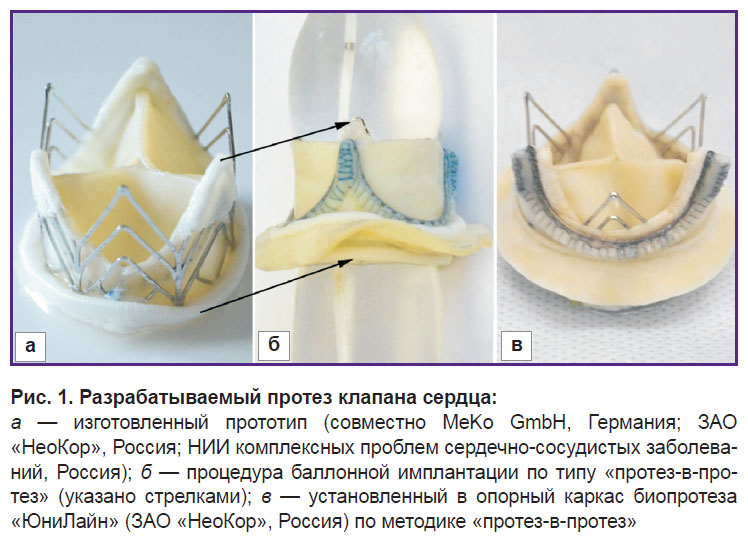
Объект исследования. В работе оценивали усталостную прочность опорных каркасов экспериментального протеза клапана сердца, разрабатываемого в Научно-исследовательском институте комплексных проблем сердечно-сосудистых заболеваний (Кемерово), который предназначен для репротезирования несостоятельного протеза по типу «протез-в-протез» (патент РФ №156774 от 19.01.16) (рис. 1, а). Имплантацию протеза осуществляют в опорный каркас протеза клапана сердца, в котором развилась дисфункция, с использованием бесшовной фиксации за счет баллонной технологии — по типу «протез-в-протез». Данная технология, основанная на стентоподобном поведении протеза, позволяет не удалять вышедший из строя протез, сокращая время и объем вмешательства.

---

Рис. 1. Разрабатываемый протез клапана сердца: а — изготовленный прототип (совместно MeKo GmbH, Германия; ЗАО «НеоКор», Россия; НИИ комплексных проблем сердечно-сосудистых заболеваний, Россия); б — процедура баллонной имплантации по типу «протез-в-протез» (указано стрелками); в — установленный в опорный каркас биопротеза «ЮниЛайн» (ЗАО «НеоКор», Россия) по методике «протез-в-протез»

---

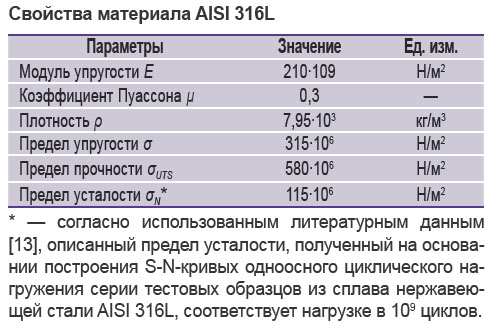
В работе исследовали модели полной линейки типоразмеров изделия: протезы от 19-го до 33-го типоразмера (всего 8 моделей). Опорный каркас данного протеза представляет собой конструкцию цилиндрической формы, стенки его имеют ячеистую структуру закрытого и открытого типов. Опорный каркас протеза изготавливают методом лазерного раскроя на основе трубы заданной толщины и диаметра из нержавеющей стали медицинского назначения AISI 316L (см. рис. 1, 2). Механический отклик материала описан упругопластической моделью с изотропным упрочнением. Прочностные и усталостные характеристики материала приведены в таблице [12].

---

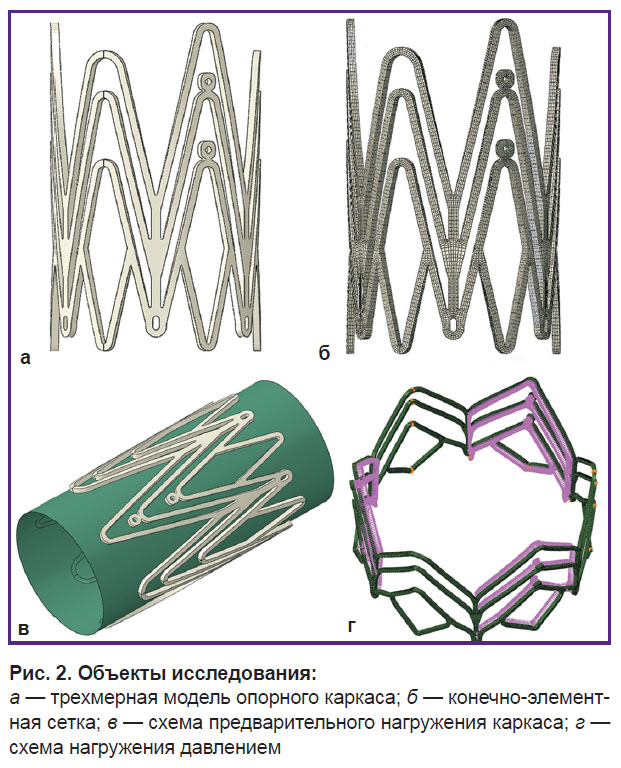
Рис. 2. Объекты исследования: а — трехмерная модель опорного каркаса; б — конечно-элементная сетка; в — схема предварительного нагружения каркаса; г — схема нагружения давлением

---

Свойства материала AISI 316L

---

Конечно-элементный анализ. Исследование проводили в среде инженерного анализа SIMULIAAbaqus (США). Исходные CAD-модели опорных каркасов были импортированы в препостпроцессор Abaqus/CAE и аппроксимированы трехмерными восьмиузловыми конечными элементами с полным интегрированием (C3D8R). Общая размерность конечно-элементной модели — 48 576 элементов со средними линейными размерами 0,125×0,125×0,125 мм.

Протез клапана сердца в процессе эксплуатации подвергается двум основным типам воздействия: процедуре имплантации за счет баллона (рис. 1, б) и нагрузкам в имплантированном состоянии (рис. 1, в) за счет действия кровотока в цикле «систола–диастола». В первом случае воздействия опорному каркасу изделия придают рабочую — имплантированную — геометрию, с помощью баллонной технологии изменяя его исходный диаметр (15 мм) до конечного (19–33 мм). В ходе данной процедуры происходит накопление пластической деформации и «закрепление» рабочей геометрии. В результате процедуры имплантации опорный каркас имеет ненулевое напряженно-деформированное состояние, связанное с работой конструкции в упругопластической зоне, которое в значительной мере влияет на последующую оценку усталостной прочности [14, 15]. Действие циклической нагрузки обусловлено давлением тока крови на опорный каркас и на створчатый аппарат, оно не способно вызвать существенного повышения среднего напряжения, однако оказывает значимое воздействие при пересчете на большое количество циклов (200 млн.). С учетом того, что опорный каркас в процессе своего жизненного цикла подвержен двум типам воздействия — имплантации и циклической нагрузке, исследование осуществляли в два последовательных этапа. Первый этап — моделирование имплантации. Он состоял из двух шагов:

расширение исследуемой модели баллоном, представляющим собой цилиндрическую поверхность из 2200 элементов SFM3D4-типа, до необходимого наружного диаметра;

приложение обратной нагрузки к баллону для оценки рекойл-эффекта конструкции и формирование окончательного напряженно-деформированного состояния системы.

Второй этап — оценка усталостной прочности, нагружение моделей эквивалентом кровотока. В качестве нагрузки использовали давление, прикладываемое к внутренней стороне каркаса в области комиссуральных стоек. Тестирование усталостной прочности осуществляли в условиях нормо- и гипертензивного давления при 70 ударах в минуту. Характер приложения давления соответствовал таковому для аортальной (для протезов 19–25 мм) и митральной (для протезов 27–33 мм) позиций: в случае нормотензивного давления эквивалент давления составлял 80 и 120 мм рт. ст.; в случае гипертензивного — 110 и 180 мм рт. ст. соответственно. Принимая во внимание особенность имплантации исследуемого объекта (в каркас несостоятельного протеза), все радиальные перемещения кнаружи от центральной оси были ограничены, т.е. использовали отнулевой цикл регулярного нагружения с коэффициентом асимметрии R=0.

Анализируемые показатели. На первом этапе исследования использовали эквивалентные напряжения по Мизесу, являющиеся типичной характеристикой для пластичных материалов. Дополнительно оценивали радиальные перемещения при максимальном раскрытии каркаса и после снятия нагрузки для расчета относительных значений возврата конструкции в результате работы эластической компоненты напряжения, т.е. упругого рекойла.

Оценку усталостной прочности проводили на основе диаграммы Гудмана, рекомендованной FDA для подобного рода анализа [13–15]. Данный метод реализует концепцию бесконечного ресурса — Infinite Fatigue Life (IFL). Проводится учет следующих характеристик рабочего цикла: среднего напряжения σ_m и переменного напряжения в рамках одного цикла σ_а. Для построения диаграммы требуются данные предела прочности материала σ_UTS и предела усталости σ_N.

σ_а/σ_N+σ_m/σ_UTS=1.

Проведено вычисление коэффициента Гудмана и его распределения по конечно-элементной модели изделия для возможности оценки наиболее критических с точки зрения усталостной прочности элементов конструкции.

Результаты

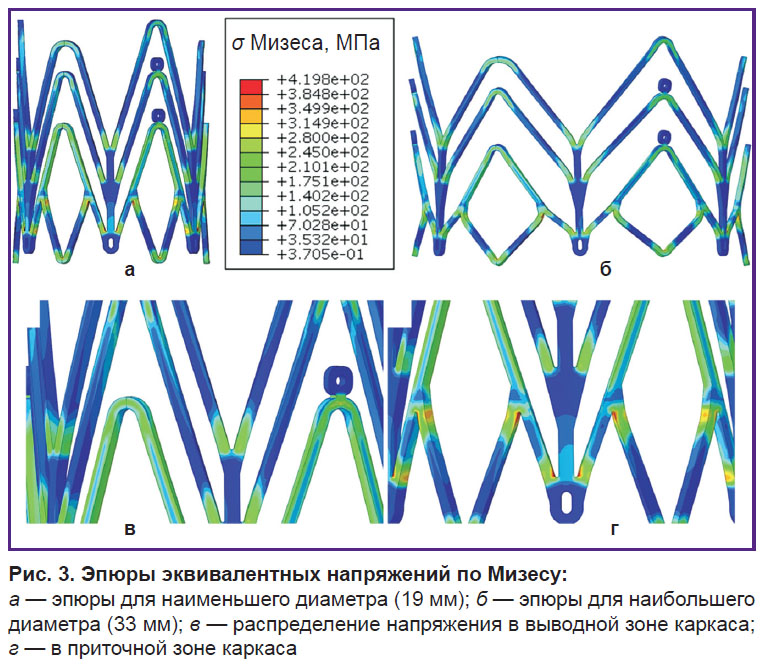
Имплантация. В ходе процесса имплантации опорного каркаса выявлен существенный рост механических напряжений в вершинах ячеек с образованием упругопластических шарниров. Максимальные значения напряжения были зафиксированы для конструкции наибольшего типоразмера — 33 мм, минимальные — для 19 мм (419,8 и 307,3 МПа соответственно). Стоит отметить, что наиболее нагруженные узлы были расположены в приточной зоне протеза (рис. 3).

---

Рис. 3. Эпюры эквивалентных напряжений по Мизесу: а — эпюры для наименьшего диаметра (19 мм); б — эпюры для наибольшего диаметра (33 мм); в — распределение напряжения в выводной зоне каркаса; г — в приточной зоне каркаса

---

Рекойл-эффект, наблюдаемый после снятия нагрузки с опорного каркаса, был незначительным как для больших, так и для и малых диаметров конструкции, и колебался в диапазоне от 4,2 до 4,48%.

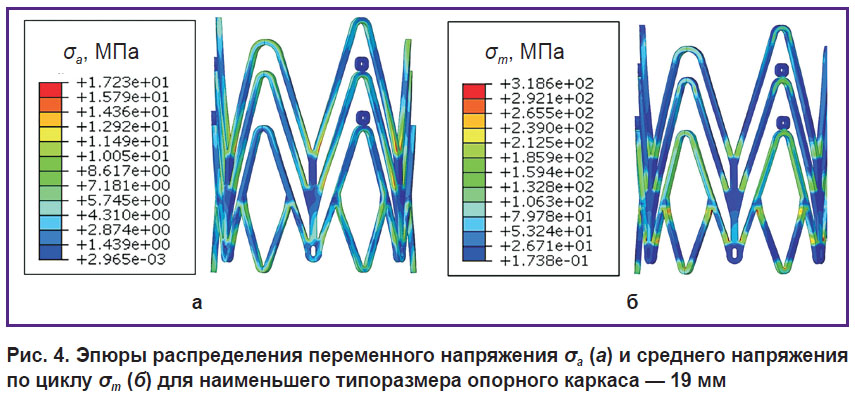
Оценка усталостной прочности. Анализ усталостной прочности опорного каркаса продемонстрировал незначительные значения переменного напряжения — показателя, обусловленного моделированием давления в цикле «нагрузка–разгрузка» (σ_a). Максимум показателя наблюдали при гипертензивном давлении для типоразмера 19 мм — 17,2 МПа (рис. 4, а), минимальное значение σ_a составило 6,3 МПа. Параметр, характеризующий суммарное напряжение, которое возникает в результате имплантации и действия переменной нагрузки — среднее напряжение цикла, — составил 314,6–425,0 МПа (рис. 4, б).

---

Рис. 4. Эпюры распределения переменного напряжения σa (а) и среднего напряжения по циклу σm (б) для наименьшего типоразмера опорного каркаса — 19 мм

---

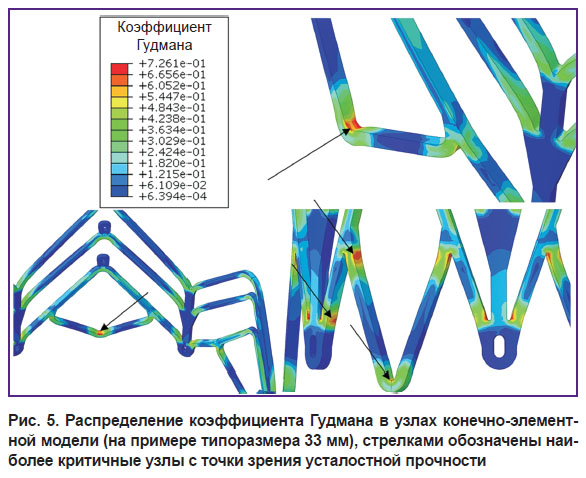
Коэффициент Гудмана и его распределение на эпюрах позволили охарактеризовать наличие и расположение наиболее критических точек опорных каркасов. Значения максимума данного показателя колебались от 0,46 до 0,72. При этом эпюры демонстрировали расположение узлов с высоким значением коэффициента в зонах стыков и изгибов конструкции (рис. 5).

---

Рис. 5. Распределение коэффициента Гудмана в узлах конечно-элементной модели (на примере типоразмера 33 мм), стрелками обозначены наиболее критичные узлы с точки зрения усталостной прочности

---

Обсуждение

Имплантация. Анализ поведения конструкции в процессе имплантации продемонстрировал значительный рост напряжений в узлах элементов (до 419,8 МПа) с переходом в зону пластической деформации, т.е. со значительным превышением предела упругости (330 МПа). Однако данный эффект является ожидаемым, так как описанный рост напряжения выше предела упругости позволяет баллонорасширяемым конструкциям сохранять и поддерживать свою геометрию после снятия нагрузки — действия баллона. С другой стороны, полученные значения напряжения Мизеса в наиболее критическом случае — 419,8 МПа (для 33 мм) — не превышали предел прочности материала σ_UTS=670 MПa, т.е. не вызывали необратимых разрушений и возникновения трещин или микротрещин. Исходя из описанных результатов можно предполагать, что процесс радиального расширения каркаса баллоном во время имплантации является безопасным для конструкции. В то же время возникающий рекойл-эффект, характерный для всех баллонорасширяемых стентоподобных конструкций [16, 17], который составляет в работе до 4,48% от конечного диаметра, может вносить коррективы в подбор типоразмера каркаса, выбираемого для имплантации.

Качественный анализ распределения напряжения Мизеса на эпюрах в исследуемых опорных каркасах продемонстрировал его неоднородность — наименее нагруженные узлы расположены в выводной зоне каркаса. Такое распределение зон ожидаемо, так как в выводной части каркаса ячейки имеют более длинные балки и меньшее количество узлов-соединений (см. рис. 1, а).

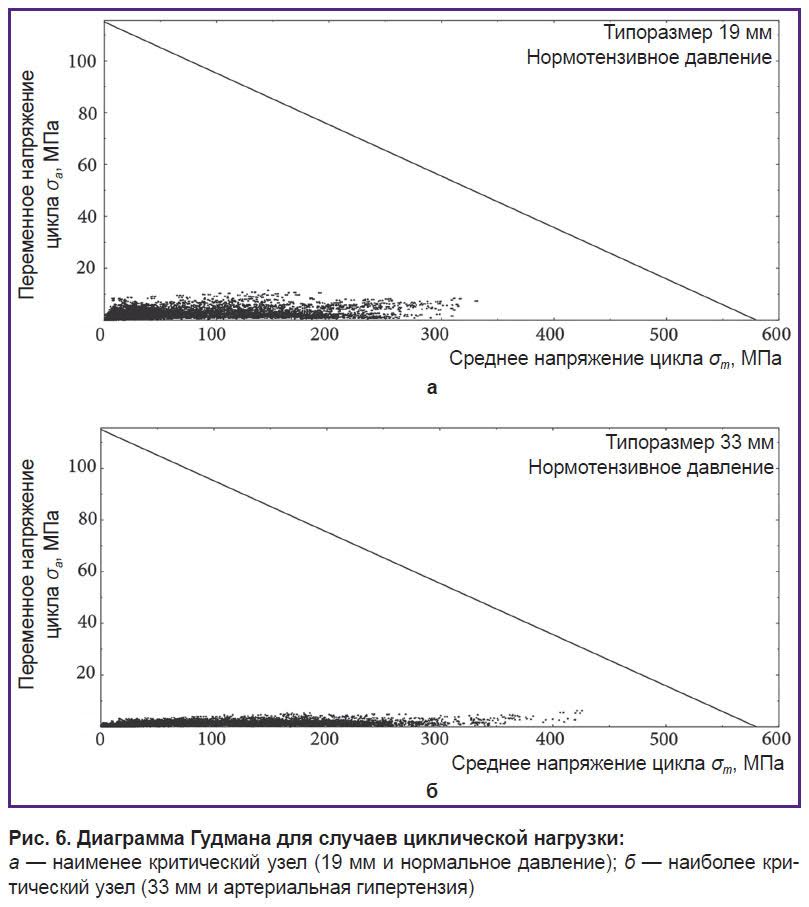
Оценка усталостной прочности. Анализ переменного напряжения по циклу «нагрузка–разгрузка» σ_a, а также среднего напряжения в опорном каркасе σ_m показал, что данные показатели были значительно ниже предела усталости материала σ_N=278 МПа и предела прочности материала σ_UTS=670 MПa, т.е. не вызывали возникновения повреждения в конструкции на протяжении 10⁹ циклов. Данное заключение подтверждается и диаграммой Гудмана: анализ показателя усталостной прочности для различных режимов продемонстрировал неспособность конструкции превысить границу области бесконечного ресурса, в том числе в условиях моделирования артериальной гипертензии. То есть все узлы опорного каркаса находятся в зоне «бесконечного ресурса» (ниже линии, рис. 6) и способны выдержать 10⁹ циклов нагрузки.

---

Рис. 6. Диаграмма Гудмана для случаев циклической нагрузки: а — наименее критический узел (19 мм и нормальное давление); б — наиболее критический узел (33 мм и артериальная гипертензия)

---

Качественный анализ диаграмм Гудмана показал, что напряжение в узлах конструкции распределено неравномерно в зависимости от типоразмера. Так, узлы на диаграмме для наименьшего размера (19 мм) расположены более компактно по оси Х, т.е. имеют бо́льшую однородность по показателю среднего напряжения цикла σ_m. В то же время по оси Y узлы распределены широко, т.е. переменное напряжение σ_aоказывает бóльший эффект на конструкции малого диаметра. Обратная зависимость наблюдается для бóльших типоразмеров (рис. 6, б).

Таким образом, вклад показателя, изучаемого на первом этапе (имплантация каркаса), в напряженно-деформируемое состояние больше для бо́льших типоразмеров, так как значительнее повышает среднее напряжение цикла σ_m. Вклад непосредственно циклической нагрузки больше в случае малых каркасов, так как повышает переменное напряжение σ_a.

Наличие в элементах конструкции узлов с высокими значениями коэффициента Гудмана (до 0,72) свидетельствует о значительной неоднородности распределения напряжения в опорном каркасе, т.е. наличии критических узлов. Однако данный коэффициент не превышает 1,00 — границы области бесконечного ресурса. Несмотря на безопасность подобных элементов с точки зрения усталостной прочности, корректировка дизайна и снижение максимума описанного коэффициента для конструкции способны дополнительно обезопасить применение протеза.

Заключение. Результаты исследования на основе метода диаграмм Гудмана продемонстрировали, что разработанный стентоподобный дизайн опорного каркаса протеза, предназначенного для репротезирования несостоятельного протеза по типу «протез-в-протез», обеспечивает ресурс усталости не менее 10⁹ циклов. Геометрия каркаса, сочетающая открытый и закрытый типы ячеек, позволяет неравномерно распределять нагрузки в зависимости от функционального назначения зон. Описанный метод анализа усталостной прочности может быть использован при расчете надежности конструкций протезов клапанов сердца на основе стентового каркаса.

Финансирование исследования. Исследование проведено в рамках финансирования по гранту Фонда содействия развитию малых форм предприятий в научно-технической сфере по теме «Разработка и испытание конструкции опорного каркаса и створчатого аппарата протеза клапана сердца для имплантации по типу “протез-в-протез”» (1-й этап проекта 22744).

Конфликт интересов отсутствует.