Informational and Statistical Analysis of Heart Rate Variability in the Assessment of the Human Vegetative Nervous System Functional State
The aim of the investigation is to study the potential of the informational and statistical method in the analysis of heart rate variability in assessing functional state of the vegetative nervous system, and to develop criteria for evaluating the degree of self-organization of the processes controlling cardiac activity and tone state.
Materials and Methods. The investigation included 156 people of both genders, which were divided into three groups. Group 1 (n=60) comprised practically healthy individuals aged 18–23 years, group 2 (n=38) included practically healthy individuals aged 32–60 years, and group 3 (n=58) consisted of patients with the diagnosis of “acute cerebral circulatory disorder, stroke”. Electrocardiograms recording with the following plotting of cardiointervalograms and their analysis were performed using electrocardiograph Poli-Spectrum-8 (Neurosoft, Russia), programs Poli-Spectrum and Poli-Spectrum-Rhythm, as well as programs especially developed by the authors for computation of Dirichlet distribution parameters.
Results. For practically healthy people the state of regulatory systems with the dominance of self-organization processes and parasympathetic nervous system tone prevailed. Self-organization coefficient S equal to one is a sort of a boundary between a normal state of the human organism regulatory systems and conditions caused by insufficiency or inadequacy of the adaptive systems, for which its value becomes less than one. While a self-organization coefficient evaluates a general state of the human adaptive regulatory systems, a coefficient of the tone state determines the character of cardiovascular system functioning. Regulatory systems having the values of self-organization coefficient and tone coefficient below one may be considered to be in a critical state.
Conclusion. Informational and statistical approach to the analysis of heart rate variability allows a more precise evaluation of the functional regulatory systems condition in comparison with the traditional methods of heart rate variability analysis.
Investigations of heart rate variability (HRV) have been drawing attention of the scientists and physicians for several decades as rather a simple method of receiving reliable information (one lead electrocardiogram recording) on the processes going in the organism as a whole and in the cardiovascular system alone. At present, classic methods of receiving and interpreting the HRV parameters have been formed [1–6].
In our opinion, however, the main problem of such investigations lies in the fact that the applied methods of mathematic processing of time series analyze the parameters (statistical, spectral, nonlinear, etc.) of the time series, but not the state of the analyzed system. If we approach to the analysis of the human cardiovascular system on the basis of investigating the states, then the processes determining them may be presented by a statistical model (image) in the form of probability distribution. Such presentation, according to thermodynamic concept of information, suggested by Claude Shannon [7], allows to consider the processes, going on in the analyzed system, in terms of thermodynamics and one of its most important concept — entropy. For our discussion it is important, that entropy as a universal function of the substance state consists of production and flow [8]. The flow characterizes the exchange (of the substance or energy) of the object with the external environment, whereas production is part of entropy, determined by the running irreversible processes.
If heart rate regulation system is regarded using autonomic and central contours as the two functional systems [9], then a statistical model of such system may be presented as beta-distribution with the function of probability density

| where |
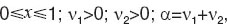
|
and entropy

|
where |

|
It has been previously shown [10], that application of parameters of informational entropy of beta-distribution instead of traditional parameters describing HRV enables us to determine more clearly differences between healthy and sick people with vascular cerebral diseases. However, simplifications lying in the basis of this model make formula (1) incapable of reflecting the system of circulatory regulation as a multi-contour hierarchical self-organizing system, which is characterized by nonlinearity, complexity and openness. Dirichlet distribution, a one-dimension analog of which is the above-mentioned model — beta-distribution (1) — was suggested as a model of multi-contour system for evaluation of the states of human adaptive regulatory systems according to HRV parameters [11]. As a statistical model Dirichlet distribution reflects the result of joint realization n-1 of independent processes xj, going on with the velocities (intensities) vj, and a process, contrary by its meaning, running with vn velocity. In this regard, the distribution informationally is equivalent to the object of any nature and complexity degree, including blood circulatory system. The function of probability density of Dirichlet distribution, determined on k-dimensional simplex, equals to

| where |

|
Dirichlet distribution entropy may be presented as a sum

in which always positive summand

represents entropy production, satisfying the second law of thermodynamics, whereas a summand

corresponds to the entropy flow, responsible for the processes of interaction with the external environment, and may have both positive and negative values. On the basis of external entropy property of Dirichlet distribution, integral index of adaptive capabilities of the human organism, a coefficient of adaptation (Ac), has been chose

where  is a total quantity of cardiointervals (R–R intervals) of two-dimensional, three-dimensional, four-dimensional, five-dimensional and other Dirichlet models, found during the analyzed period in the time series, having negative values of external entropy, and
is a total quantity of cardiointervals (R–R intervals) of two-dimensional, three-dimensional, four-dimensional, five-dimensional and other Dirichlet models, found during the analyzed period in the time series, having negative values of external entropy, and  is a total quantity of cardiointervals of two-dimensional, three-dimensional, four-dimensional, five-dimensional, and other Dirichlet models, found during the analyzed period in the time series, having positive values of external entropy.
is a total quantity of cardiointervals of two-dimensional, three-dimensional, four-dimensional, five-dimensional, and other Dirichlet models, found during the analyzed period in the time series, having positive values of external entropy.
However, the coefficient of adaptation Ac, suggested previously by the authors [11], does not adequately take into consideration the contribution of Dirichlet models of various dimensions, making it impossible to assess reliably the degree of self-organization of the processes controlling cardiac activity, which may become a sensible criterion of the body regulation system state at a definite point of time.
The aim of the investigation is to work out criteria for assessing the degree of self-organization of the processes controlling cardiac activity and the state of vegetative nervous system tone on the basis of informational and statistical approach to the analysis of heart rate variability, taking into account the contribution to the regulation the activity of parasympathetic and sympathetic branches of the autonomic nervous system.
Materials and Methods. Three groups took part in the investigation: a group (n=60) of practically healthy young people of both genders aged 18–23 years, a group (n=38) of practically healthy people aged 32–60 years and a group (n=58) of patients with cerebral circulatory disorders (with a diagnosis “acute cerebral circulatory disorder, stroke”).
The study complies with the Declaration of Helsinki (the Declaration was passed in Helsinki, Finland, June, 1964, and revised in October, 2000, Edinburg, Scotland) and was performed following approval by the local ethic committee. Written informed consent was obtained from every patient.
Electrocardiograms were taken according to the recommendations [1, 5] using electrocardiograph Poli-Spectrum-8 (Neurosoft, Russia). Building up cardiointervalograms and data analysis were performed using programs Poli-Spectrum and Poli-Spectrum-Rhythm, and original programs especially developed for calculation of Dirichlet distribution parameters. The degree of self-organization of the processes controlling cardiac activity, in contrast to [11], was assessed by the value of the self-organization coefficient Sc:

where  is a total weighted quantity of cardiointervals of Dirichlet models of i-dimension, found during the analyzed period in the time series, having a negative value of external entropy, and
is a total weighted quantity of cardiointervals of Dirichlet models of i-dimension, found during the analyzed period in the time series, having a negative value of external entropy, and  is a total weighted quantity of Dirichlet models, found during the analyzed period in the time series, having a positive value of external entropy.
is a total weighted quantity of Dirichlet models, found during the analyzed period in the time series, having a positive value of external entropy.
The state of the autonomic nervous system tone was evaluated traditionally by the ratio of the high-frequency heart rates in the spectrogram to the low-frequency rates (LF/HF) [7, 8], and also by the ratio of the number of the self-organization processes of the heart rate regulation system involving parasympathetic nervous system to the number of the same processes involving sympathetic nervous system, i.e. by the value of the coefficient Ti, for which the following ratio has been chosen by the authors:

where  is a total weighted quantity of cardiointervals of two-dimensional, three-dimensional and four-dimensional Dirichlet models found in the time series, having a negative value of external entropy, and
is a total weighted quantity of cardiointervals of two-dimensional, three-dimensional and four-dimensional Dirichlet models found in the time series, having a negative value of external entropy, and  is a total weighted quantity of Dirichlet models with a negative external entropy of dimensions from five- to fourteen-dimensional.
is a total weighted quantity of Dirichlet models with a negative external entropy of dimensions from five- to fourteen-dimensional.
Methodologically, the result was achieved in the following way: a sequence of cardiointerval samples of n-volume was chosen from the cardiointervalogram of N values volume moving by one value. Values of the asymmetry coefficient and excess index were determined for each obtained sample, which then were used to find the sequence of beta-distributions (1). In accordance with the rules of informational and statistical theory, set forth in the work [12], from the following one after another beta-distributions we proceeded to the sequence of Dirichlet distributions.
Statistical verification of the hypotheses was done using Student t-criterion and MS Excel program.
Results. Classification of the practically young people by the groups according to Ti parameter: vagotonic type (Ti>1.3) — 13 persons, normotonic type (1<Ti<1.3) — 12, and sympathicotonic type (Ti<1) — 9 persons showed statistically significant (p<0.01) differences in the mean values of Dirichlet model dimensions between the groups of vagotonic–sympathicotonic, vagotonic–normotonic, and normotonic–simpathicotonic types of persons, and also in the mean values of the ratio of the low frequency component of the HRV spectrum (LF) to the high frequency component (HF) between the groups of normotonic–sympathicotonic and vagotonic–sympathicotonic types.
Usage of LF/HF parameter for classification of the young men into groups: vagotonics (LF/HF<0.8) — 12 persons, normotonics (0.8<LF/HF<1.7) — 13 persons, and sympathicotonics (LF/HF>1.7) — 9 persons — showed statistically significant (p<0.01) differences in the mean values of Dirichlet model dimensions only between the groups of vagotonics–sympathicotonics and normotonics–sympathicotonics.
Successive application of Ti and LF/HF parameters to this group of young people in classifying the type of vegetative regulation allowed identification of the group of typical vagotonics (Ti>1, LF/HF<0.8) — 9 people, typical normotonics (Ti≈1, 0.8<LF/HF<1.7) — 5 people, and typical sympathicotonics (Ti<1, LF/HF>1.7) — 5 people.
Determination of the relative weighted quantity of Dirichlet model cardiointervals, found in the time series, having a negative value of external entropy of dimensions 2–4 and 5–14 for typical vagotonics, normotonics, and sympathicotonics (Figure 1) demonstrated, that predominance of cardiointervals of Dirichlet models weighted quantity with a negative external entropy of dimension 2–4 in the time series is characteristic of typical vagotonics. In this case coefficient Ti is essentially greater than one for the state with a marked activity of the parasympathetic branch of the vegetative nervous system. For the typical normotonics there is a relative equality of contribution of weighted quantity of Dirichlet models of the small (2–4) and large (5–14) dimensions to the processes of self-organization, whereas predominance of Dirichlet models with 5–14 dimensions at Ti<1 is characteristic of typical sympathicotonics.
 Figure 1. The ratio of Dirichlet models of dimensions 2–4 and 5–14 (in percentage) among the young people with a different tone of the autonomic nervous system Figure 1. The ratio of Dirichlet models of dimensions 2–4 and 5–14 (in percentage) among the young people with a different tone of the autonomic nervous system
|
In order to test the application of self-organization coefficients Sc and Ti for the assessment of the autonomic regulation system state, parameters of the three groups of people have been analyzed: practically healthy young people at the age of 18–23 years, practically healthy people at the age of 32–60 years and sick people aged 32–60 years with acute cerebral circulatory disorder (Figure 2).
 Figure 2. Results of the analysis of the autonomic regulation system state using informational and statistical parameters Sc and Ti Figure 2. Results of the analysis of the autonomic regulation system state using informational and statistical parameters Sc and Ti
|
The state of the body regulatory systems in the group of practically healthy young people was determined by the predominance of self-organization processes (Sc>1) in the majority of the examined persons, in 64% of which the tone of the parasympathetic nervous system (Sc>1, Ti>1) was increased. The number of people with a normal self-organization of the regulatory systems slightly diminishes (by 10%) with age, as well as the proportion of people with predominance of parasympathetic system tone.
In the group of patients with acute cerebral circulatory disorder the processes of self-organization are preserved only in 46% of the examined individuals with the larger quantity of people with a high tone of the sympathetic nervous system and absence of the self-organization processes of the regulatory systems (35% of cases).
Thus, according to the degree of significance of the contribution of the autonomic nervous system to the regulation of the blood circulation the investigated parameters were distributed in the following descending order: Ti, LF/HF, as shown by the analysis of the heart rate.
The coefficient of self organization Sc equal to one is a sort of a boundary between a normal state of the human organism regulatory systems and conditions caused by insufficiency or inadequacy of the adaptive systems, for which its value becomes less than one.
The states of the autonomic nervous system may be considered to be critical, when the values of self-organization coefficient Sc and tone coefficient Ti are below one.
Conclusion. The informational and statistical approach to the analysis of the heart rate variability enables one to assess more precisely a functional state of the body regulatory systems compared to the traditional methods of the HRV analysis. This fact may be of great importance for evaluating biological and social adaptation of a man to different environmental and life conditions, assessment of reactivity and stability of the organism under various extreme exposures.
Study Funding and Conflicts of Interest. This study was not supported by any financial sources and there is no topic specific conflict of interest related to the authors of this study.
References
- Malik M., Bigger J.T., Camm A.J., Kleiger R.E., Malliani A., Moss A.J., Schwartz P.J. Нeart rate variability. Standards of measurement, physiological interpretation, and clinical use. Task Force of the European Society of Cardiology and the North American Society of Pacing and Electrophysiology. European Heart Journal 1996; 17(3): 354–381.
- Baevskiy R.M., Ivanov G.G., Chireykin L.V., et al. Analiz variabel’nosti serdechnogo ritma pri ispol’zovanii razlichnykh elektrokardiograficheskikh sistem. V kn.: Variabel’nost’ serdechnogo ritma: teoreticheskie aspekty i prakticheskoe primenenie. Tezisy dokladov Mezhdunarodnogo simpoziuma [Analysis of heart rate variability using various electrocardiographic systems. In: heart rate variability: theoretical aspects and practical application. Abstracts of International symposium]. Izhevsk: UdmGU; 2003; p. 201–255.
- Goldberger A.L., West B. J. Applications of nonlinear dynamics to clinical cardiology. Ann N Y Acad Sci 1987; 504: 195–213, http://dx.doi.org/10.1111/j.1749-6632.1987.tb48733.x.
- Peng C.-K., Havlin S., Stanley H.E., Goldberger A.L. Quantification of scaling exponents and cross over phenomena in nonstationary heartbeat time series. Chaos 1995; 5(1): 82–87, http://dx.doi.org/10.1063/1.166141.
- Task Force of the European Society of Cardiology and the North American Society of Pacing and Electrophysiology. Heart rate variability. Standards of measurement, physiological interpretation and clinical application. Vestnik aritmologii 1999; 11: 53–78.
- Mironova T.F., Mironov V.A. Klinicheskiy analiz volnovoy struktury sinusovogo ritma serdtsa [Clinical analysis of the cardiac sinus rhythm wave structure]. Chelyabinsk: Chelyabinskiy Dom pechati; 1998.
- Shannon C.E., Weaver W. The mathematical theory of communications. Urbana: University of Illinois Press; 1949.
- Prigogine I. Time, structure, and fluctuation. Uspekhi fizicheskikh nauk 1980; 131(2): 185–207, http://dx.doi.org/10.3367/UFNr.0131.198006a.0185.
- Baevskiy P.M., Parin V.V. Vvedenie v meditsinskuyu kibernetiku [Introduction to medical cybernetics]. Moscow: Meditsina; 1966.
- Mukhina I.V., Levanov V.M., Kovaleva G.V., Shirokiy G.B., Ilyakhinskiy A.V., Kulikov D.D. A diagnostic value of the heart rate variability analysis based on the assessment of information entropy of beta-distribution in evaluation of patients with cerebral vascular diseases. Funktsional’naya diagnostika 2013; 1: 47–54.
- Shirokiy G.B., Ilyakhinskiy A.V., Levanov V.M., Mukhina I.V. Dirichlet distribution as a model of the state of adaptation regulatory human body systems in analyzing heart rate variability. Klinicheskaya telematika i telemeditsina 2013; 10(9): 75–78.
- Sereda Yu.S. Problemy informatsionno-statisticheskoy teorii [Problems of informational and statistical theory]. Nizhny Novgorod: OOO “Tipografiya “Povolzh’e”; 2007; 356 p.










